Advertisements
Advertisements
प्रश्न
Observe all the four triangles FAB, EAB, DAB and CAB as shown in the given figure.

- All triangles have the same base and the same altitude.
- All triangles are congruent.
- All triangles are equal in area.
- All triangles may not have the same perimeter.
उत्तर
1. True.
It is clear from the figure that all triangles have same base AB and all the vertices lie on the same line, so the distance between vertex and base of triangle (i.e. length of altitude) are equal.
2. False
It is clear from the figure that all triangles have only base line is equal and no such other lines are equal to each other.
3. True
Because the triangles on same base and between same parallel lines have equal in area.
4. True
It is clear from the figure that all triangles may not have the same perimeter.
APPEARS IN
संबंधित प्रश्न
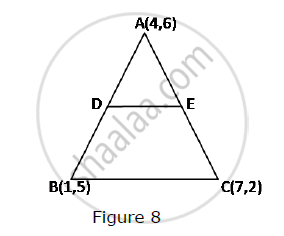
In Fig. 8, the vertices of ΔABC are A(4, 6), B(1, 5) and C(7, 2). A line-segment DE is drawn to intersect the sides AB and AC at D and E respectively such that `(AD)/(AB)=(AE)/(AC)=1/3 `Calculate th area of ADE and compare it with area of ΔABCe.
Find the area of the quadrilateral whose vertices, taken in order, are (-4, -2), (-3, -5), (3, -2) and (2, 3).
Find the centre of a circle passing through the points (6, − 6), (3, − 7) and (3, 3).
Find the missing value:
| Base | Height | Area of triangle |
| 15 cm | ______ | 87 cm2 |
The vertices of ΔABC are (−2, 1), (5, 4) and (2, −3) respectively. Find the area of the triangle and the length of the altitude through A.
Find the centroid of the triangle whosw vertices is (1,4), (-1,1) and (3,2) .
Using integration, find the area of triangle ABC, whose vertices are A(2, 5), B(4, 7) and C(6, 2).
If the points (3, -2), (x, 2), (8, 8) are collinear, then find the value of x.
Find the area of the triangle whose vertices are (–8, 4), (–6, 6) and (–3, 9).
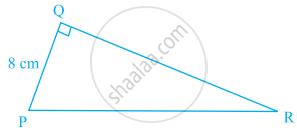
Area of a triangle PQR right-angled at Q is 60 cm2 in the figure. If the smallest side is 8 cm long, find the length of the other two sides.