Advertisements
Advertisements
प्रश्न
Using integration, find the area of triangle ABC, whose vertices are A(2, 5), B(4, 7) and C(6, 2).
उत्तर
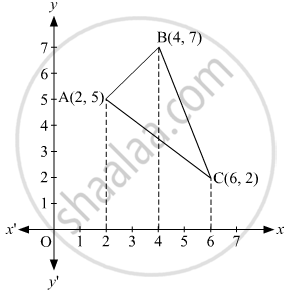
Vertices of the given triangle are A(2,5), B(4,7), and C(6,2).
Equation of AB
`y - 5 = (7-5)/(4-2) (x -2)`
⇒ `y - 5 = x -2`
⇒ `y = x + 3`
Let's say y1= x+3
Equation of BC:
`y -7= (2-7)/(6-4)(x-4)`
⇒ `y = (-5)/(2) (x-4) +7=(-5)/(2) x+17`
Let's say `y_2 = -(5)/(2)x+17`
Equation of AC:
`y -5 = (2-5)/(6-2) (x-2)`
⇒ `y = (-3)/(4)(x-2)+5 = (-3)/(4)x+13/2`
Let's say `y_3 = (-3)/(4)x+13/2`
`"ar" (Δ"ABC") = int_2^4 y_1 dx + int_4^6 y_2 dx - int_2^6 y_3 dx`
= `int_2^4 (x+3) dx + int_4^6 ((-5)/2 x+17) dx -int_2^6 (-3)/4 x+13/2)dx`
= `[x^2/2 + 3x]_2^4 + [(-5x^2)/4 + 17x]_4^6 - [(-3x^2)/8 + (13x)/2]_2^6`
= `[16/2 + 12 - 4/2 -6]+[(-180)/4 + 102+80/4-68]-[(-108)/8+78/2+12/8-26/2]`
= 12 + 9 - 14
= 7 sq units.
APPEARS IN
संबंधित प्रश्न
A(4, - 6), B(3,- 2) and C(5, 2) are the vertices of a 8 ABC and AD is its median. Prove that the median AD divides Δ ABC into two triangles of equal areas.
The perimeter of a right triangle is 60 cm. Its hypotenuse is 25 cm. Find the area of the triangle.
If the points A(x, 2), B(−3, −4) and C(7, − 5) are collinear, then the value of x is:
(A) −63
(B) 63
(C) 60
(D) −60
If A(−4, 8), B(−3, −4), C(0, −5) and D(5, 6) are the vertices of a quadrilateral ABCD, find its area.
Find the area of the triangle PQR with Q(3,2) and the mid-points of the sides through Q being (2,−1) and (1,2).
If D, E and F are the mid-points of sides BC, CA and AB respectively of a ∆ABC, then using coordinate geometry prove that Area of ∆DEF = `\frac { 1 }{ 4 } "(Area of ∆ABC)"`
Let A (4, 2), B (6, 5) and C (1, 4) be the vertices of ΔABC.
(i) The median from A meets BC at D. Find the coordinates of point D.
(ii) Find the coordinates of the point P on AD such that AP: PD = 2:1
(iii) Find the coordinates of point Q and R on medians BE and CF respectively such that BQ: QE = 2:1 and CR: RF = 2:1.
(iv) What do you observe?
(v) If A(x1, y1), B(x2, y2), and C(x3, y3) are the vertices of ΔABC, find the coordinates of the centroid of the triangle.
Find the area of the quadrilaterals, the coordinates of whose vertices are
(1, 2), (6, 2), (5, 3) and (3, 4)
Four points A (6, 3), B (−3, 5), C(4, −2) and D (x, 3x) are given in such a way that `(ΔDBG) /(ΔABG)=1/2,` find x
Two vertices of a triangle are (1, 2), (3, 5) and its centroid is at the origin. Find the coordinates of the third vertex.
If the coordinates of the mid-points of the sides of a triangle are (3, 4) (4, 6) and (5, 7), find its vertices.
Find the area of a triangle two sides of which are 18 cm and 10 cm and the perimeter is 42cm ?
Show that the points (-3, -3),(3,3) and C (-3 `sqrt(3) , 3 sqrt(3))` are the vertices of an equilateral triangle.
Show that the points A (3,1) , B (0,-2) , C(1,1) and D (4,4) are the vertices of parallelogram ABCD.
Find a relation between x and y, if the points A(x, y), B(-5, 7) and C(-4, 5) are collinear.
Find the area of ΔABC with vertices A(0, -1), B(2,1) and C(0, 3). Also, find the area of the triangle formed by joining the midpoints of its sides. Show that the ratio of the areas of two triangles is 4:1.
In ☐ABCD, l(AB) = 13 cm, l(DC) = 9 cm, l(AD) = 8 cm, find the area of ☐ABCD.

If the sides of a triangle are 3 cm, 4 cm and 5 cm, then the area is
The table given below contains some measures of the right angled triangle. Find the unknown values.
| Base | Height | Area |
| 5 feet | ? | 20 sq.feet |
The area of a triangle with vertices (a, b + c), (b, c + a) and (c, a + b) is ______.
The area of the triangle ABC with the vertices A(-5, 7), B(-4, -5) and C(4, 5) is ______.
Find the cost of laying grass in a triangular field of sides 50 m, 65 m and 65 m at the rate of Rs 7 per m2.
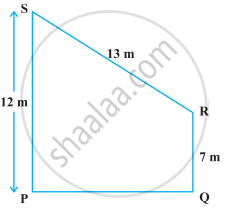
Find the area of the trapezium PQRS with height PQ given in the following figure.
Find the missing value:
| Base | Height | Area of parallelogram |
| ______ | 15 cm | 154.5 cm2 |
Find the missing value:
| Base | Height | Area of parallelogram |
| ______ | 8.4 cm | 48.72 cm2 |
The area of a triangle with vertices A, B, C is given by ______.
If (a, b), (c, d) and (e, f) are the vertices of ΔABC and Δ denotes the area of ΔABC, then `|(a, c, e),(b, d, f),(1, 1, 1)|^2` is equal to ______.
