Advertisements
Advertisements
प्रश्न
Using integration, find the area of triangle ABC, whose vertices are A(2, 5), B(4, 7) and C(6, 2).
उत्तर
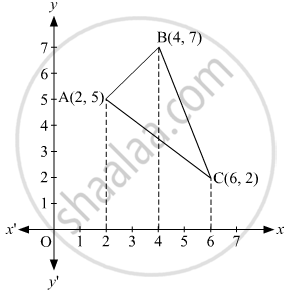
Vertices of the given triangle are A(2,5), B(4,7), and C(6,2).
Equation of AB
`y - 5 = (7-5)/(4-2) (x -2)`
⇒ `y - 5 = x -2`
⇒ `y = x + 3`
Let's say y1= x+3
Equation of BC:
`y -7= (2-7)/(6-4)(x-4)`
⇒ `y = (-5)/(2) (x-4) +7=(-5)/(2) x+17`
Let's say `y_2 = -(5)/(2)x+17`
Equation of AC:
`y -5 = (2-5)/(6-2) (x-2)`
⇒ `y = (-3)/(4)(x-2)+5 = (-3)/(4)x+13/2`
Let's say `y_3 = (-3)/(4)x+13/2`
`"ar" (Δ"ABC") = int_2^4 y_1 dx + int_4^6 y_2 dx - int_2^6 y_3 dx`
= `int_2^4 (x+3) dx + int_4^6 ((-5)/2 x+17) dx -int_2^6 (-3)/4 x+13/2)dx`
= `[x^2/2 + 3x]_2^4 + [(-5x^2)/4 + 17x]_4^6 - [(-3x^2)/8 + (13x)/2]_2^6`
= `[16/2 + 12 - 4/2 -6]+[(-180)/4 + 102+80/4-68]-[(-108)/8+78/2+12/8-26/2]`
= 12 + 9 - 14
= 7 sq units.
APPEARS IN
संबंधित प्रश्न
A(4, - 6), B(3,- 2) and C(5, 2) are the vertices of a 8 ABC and AD is its median. Prove that the median AD divides Δ ABC into two triangles of equal areas.
If the points A(−1, −4), B(b, c) and C(5, −1) are collinear and 2b + c = 4, find the values of b and c.
Prove that the points (a, b + c), (b, c + a) and (c, a + b) are collinear
For what value of k are the points (k, 2 – 2k), (–k + 1, 2k) and (–4 – k, 6 – 2k) are collinear ?
Find the area of the triangle whose vertices are: (2, 3), (-1, 0), (2, -4)
Find the area of the quadrilateral whose vertices, taken in order, are (-4, -2), (-3, -5), (3, -2) and (2, 3).
Find the area of a triangle with vertices at the point given in the following:
(−2, −3), (3, 2), (−1, −8)
The area of a triangle is 5 sq units. Two of its vertices are (2, 1) and (3, –2). If the third vertex is (`7/2`, y). Find the value of y
Find the area of the following triangle:

Find the area of the quadrilaterals, the coordinates of whose vertices are
(−3, 2), (5, 4), (7, −6) and (−5, −4)
For what value of a point (a, 1), (1, -1) and (11, 4) are collinear?
Find the centroid of the triangle whosw vertices is (1,4), (-1,1) and (3,2) .
Prove analytically that the line segment joining the middle points of two sides of a triangle is equal to half of the third side.
Find the third vertex of a ΔABC if two of its vertices are B(-3,1) and C (0,-2) and its centroid is at the origin
Find the area of ΔABC whose vertices are:
A( 3,8) , B(-4,2) and C( 5, -1)
A(7, -3), B(5,3) and C(3,-1) are the vertices of a ΔABC and AD is its median. Prove that the median AD divides ΔABC into two triangles of equal areas.
Show that the following points are collinear:
A(5,1), B(1, -1) and C(11, 4)
Find a relation between x and y, if the points A(2, 1), B(x, y) and C(7,5) are collinear.
Find the value(s) of k so that the quadratic equation x2 − 4kx + k = 0 has equal roots.
Find the value of p for which the points (−5, 1), (1, p) and (4, −2) are collinear.
The table given below contains some measures of the right angled triangle. Find the unknown values.
| Base | Height | Area |
| 20 cm | 40 cm | ? |
The points A(2, 9), B(a, 5) and C(5, 5) are the vertices of a triangle ABC right angled at B. Find the values of a and hence the area of ∆ABC.
The area of a triangle with base 4 cm and height 6 cm is 24 cm2.
The area of ∆ABC is 8 cm2 in which AB = AC = 4 cm and ∠A = 90º.
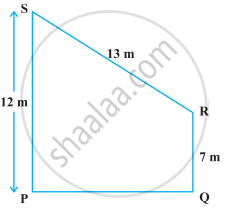
Find the area of the trapezium PQRS with height PQ given in the following figure.
Area of triangle PQR is 100 cm2 as shown in the below figure. If altitude QT is 10 cm, then its base PR is ______.

Observe all the four triangles FAB, EAB, DAB and CAB as shown in the given figure.

- All triangles have the same base and the same altitude.
- All triangles are congruent.
- All triangles are equal in area.
- All triangles may not have the same perimeter.
In the given figure, ratio of the area of triangle ABC to the area of triangle ACD is the same as the ratio of base BC of triangle ABC to the base CD of ΔACD.

Let a vector `αhati + βhatj` be obtained by rotating the vector `sqrt(3)hati + hatj` by an angle 45° about the origin in counter-clockwise direction in the first quadrant. Then the area of triangle having vertices (α, β), (0, β) and (0, 0) is equal to ______.
