Advertisements
Advertisements
प्रश्न
Find the centroid of the triangle whosw vertices is (1,4), (-1,1) and (3,2) .
उत्तर
We know that the coordinates of the centroid of a triangle whose vertices are
`(x_1,y_1),(x_2,y_2) (x_3,y_3)`are
`((x_1+x_2+x_3)/3,(y_1+y_2+y_3)/3)`
so, the coordinates of the centroid of a triangle whose vertices are
(1,4),(-1,-1) and (3,-2) are `((1-1+3)/3,(4-1-2)/3)`
`=(1,1/3)`
APPEARS IN
संबंधित प्रश्न
Find the area of the triangle formed by joining the mid-point of the sides of the triangle whose vertices are (0, –1), (2, 1) and (0, 3). Find the ratio of area of the triangle formed to the area of the given triangle.
The vertices of ΔABC are (−2, 1), (5, 4) and (2, −3) respectively. Find the area of the triangle and the length of the altitude through A.
Prove analytically that the line segment joining the middle points of two sides of a triangle is equal to half of the third side.
prove that the points A (7, 10), B(-2, 5) and C(3, -4) are the vertices of an isosceles right triangle.
Show that the points A(-5,6), B(3,0) and C(9,8) are the vertices of an isosceles right-angled triangle. Calculate its area.
Find the area of ΔABC whose vertices are:
A( 3,8) , B(-4,2) and C( 5, -1)
Show that the following points are collinear:
A(-5,1), B(5, 5) and C(10, 7)
Show that the following points are collinear:
A(5,1), B(1, -1) and C(11, 4)
Area of triangle MNO in the figure is ______.
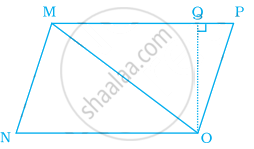
Area of a right-angled triangle is 30 cm2. If its smallest side is 5 cm, then its hypotenuse is ______.
