Question

Let A (4, 2), B (6, 5) and C (1, 4) be the vertices of ΔABC.

(i) The median from A meets BC at D. Find the coordinates of point D.

(ii) Find the coordinates of the point P on AD such that AP: PD = 2:1

(iii) Find the coordinates of point Q and R on medians BE and CF respectively such that BQ: QE = 2:1 and CR: RF = 2:1.

(iv) What do you observe?

(v) If A(x₁, y₁), B(x₂, y₂), and C(x₃, y₃) are the vertices of ΔABC, find the coordinates of the centroid of the triangle.

Answer 1

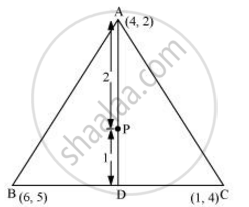
(i) Median AD of the triangle will divide the side BC into two equal parts.

Therefore, D is the mid-point of side BC

Coordinate of D = ` ((6+1)/2, (5+4)/2) = (7/2, 9/2)`

(ii) Point P divides the side AD in a ratio 2:1.

Coordinate of P =`((2xx7/2+1xx4)/(2+1), (2xx9/2+1xx2)/(2+1))= (11/3, 11/3)`

 (iii) Median BE of the triangle will divide the side AC into two equal parts.

Therefore, E is the mid-point of the side AC.

Coordinate of E =` ((4+1)/2,(2+4)/2) = (5/2, 3)`

Point Q divides the side BE in a ratio 2:1.

Coordinate of Q =`((2xx5/2+1xx6)/(2+1), (2xx3+1xx5)/(2+1)) = (11/3,11/3)`

Median CF of the triangle will divide the side AB in two equal parts. Therefore, F is the mid-point of side AB

Coordinate of F =`((4+6)/2, (2+5)/2) = (5, 7/2)`

Point R divides the side CF in a ratio 2:1.

Coordinate of R =`((2xx5+1xx1)/(2+1),(2xx7/2+1xx4)/(2+1)) = (11/3, 11/3)`

(iv) It can be observed that the coordinates of point P, Q, R are the same.

Therefore, all these are representing the same point on the plane i.e., the centroid of the triangle.

 (v) Consider a triangle, ΔABC, having its vertices as A(x₁, y₁), B(x₂, y₂), and C(x₃, y₃).

The median AD of the triangle will divide the side BC into two equal parts. Therefore, D is the mid-point of side BC.

Coordinate of D =`((x_2+x_3)/2,(y_2+y_3)/2)`

Let the centroid of this triangle be O.

Point O divides the side AD in a ratio of 2:1.

Coordinate of O = `((2xx(x_2+x_3)/2+1xxx_1)/(2+1), (2xx(y_2+y_3)/2+1xxy_1)/(2+1))`

`= ((x_1+x_2+x_3)/3, (y_1+y_2+y_3)/3)`