Advertisements
Advertisements
प्रश्न
Find the area of the triangle PQR with Q(3,2) and the mid-points of the sides through Q being (2,−1) and (1,2).
उत्तर
Let the coordinates of the vertices P and R of ∆PQR be (a1, b1) and (a2, b2), respectively.
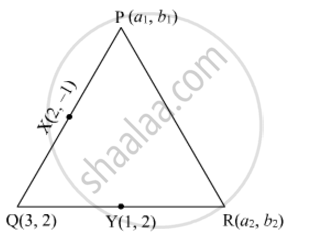
Suppose X(2, −1) is the midpoint of PQ.
Then,
`(2,-1)=((a_1+3)/2, (b_1+2)/2)`
`=>(a_1+3)/2=2 `
⇒ a1=1 and b1=−4
Therefore, the coordinates of P are (1, −4).
Again, suppose Y(1, 2) is the midpoint of QR.
Now,
`(1,2)=((a_2+3)/2,(b_2+2)/2)`
`=>(a_2+3)/2=1 `
⇒ a2=−1 and b2=2
Therefore, the coordinates of R are (−1, 2).
Thus, the vertices of ∆PQR are P(1,−4), Q(3, 2) and R(−1, 2).
Now,
Area of ∆PQR =`1/2`×[1(2−2)+3(2+4)−1(−4−2)]
=`1/2`(18+6)
=`1/2`(24)
=12
Thus, the area of ∆PQR is 12 square units.
संबंधित प्रश्न
Find the area of the triangle whose vertices are: (–5, –1), (3, –5), (5, 2)
In each of the following find the value of 'k', for which the points are collinear.
(7, -2), (5, 1), (3, -k)
Find the area of a triangle whose vertices are
`(at_1^2,2at_1),(at_2^2,2at_2)` and `(at_3^2,2at_3)`
The coordinates of the point P dividing the line segment joining the points A (1, 3) and B (4, 6) in the ratio 2 : 1 are:
Using determinants, find the values of k, if the area of triangle with vertices (–2, 0), (0, 4) and (0, k) is 4 square units.
Find the value of p for which the points (−5, 1), (1, p) and (4, −2) are collinear.

In Figure 1, PS = 3 cm, QS = 4 cm, ∠PRQ = θ, ∠PSQ = 90°, PQ ⊥ RQ and RQ = 9 cm. Evaluate tan θ.
The table given below contains some measures of the right angled triangle. Find the unknown values.
| Base | Height | Area |
| ? | 12 m | 24 sq.m |
Area of a right-angled triangle is 30 cm2. If its smallest side is 5 cm, then its hypotenuse is ______.
Area of a triangle = `1/2` base × ______.
