Advertisements
Advertisements
प्रश्न
Using determinants, find the values of k, if the area of triangle with vertices (–2, 0), (0, 4) and (0, k) is 4 square units.
उत्तर
A(ΔABC ) = 4
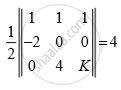
1(0-0)-1(-2K)+1(-8-0)=±8
2K - 8 = ±8
2K = ±8 + 8
∴ K =`16/2` or K=`0/2 rArr` K =8 or K = 0
APPEARS IN
संबंधित प्रश्न
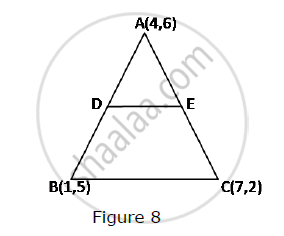
In Fig. 8, the vertices of ΔABC are A(4, 6), B(1, 5) and C(7, 2). A line-segment DE is drawn to intersect the sides AB and AC at D and E respectively such that `(AD)/(AB)=(AE)/(AC)=1/3 `Calculate th area of ADE and compare it with area of ΔABCe.
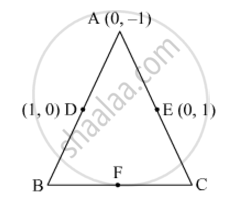
In Fig. 6, ABC is a triangle coordinates of whose vertex A are (0, −1). D and E respectively are the mid-points of the sides AB and AC and their coordinates are (1, 0) and (0, 1) respectively. If F is the mid-point of BC, find the areas of ∆ABC and ∆DEF.
Find the area of the triangle PQR with Q(3,2) and the mid-points of the sides through Q being (2,−1) and (1,2).
If D, E and F are the mid-points of sides BC, CA and AB respectively of a ∆ABC, then using coordinate geometry prove that Area of ∆DEF = `\frac { 1 }{ 4 } "(Area of ∆ABC)"`
Find the area of the triangle whose vertices are: (–5, –1), (3, –5), (5, 2)
Find the area of the quadrilateral whose vertices, taken in order, are (-4, -2), (-3, -5), (3, -2) and (2, 3).
Determine the ratio in which the line 2x + y – 4 = 0 divides the line segment joining the points A(2, – 2) and B(3, 7).
Find the area of a triangle with vertices at the point given in the following:
(2, 7), (1, 1), (10, 8)
Find the area of a triangle with vertices at the point given in the following:
(−2, −3), (3, 2), (−1, −8)
Find the area of the following triangle:

ΔABC is isosceles with AB = AC = 7.5 cm and BC = 9 cm (see the given figure). The height AD from A to BC, is 6 cm. Find the area of ΔABC. What will be the height from C to AB i.e., CE?

Find the area of a triangle whose vertices are
(a, c + a), (a, c) and (−a, c − a)
Find the area of the quadrilaterals, the coordinates of whose vertices are
(1, 2), (6, 2), (5, 3) and (3, 4)
The four vertices of a quadrilateral are (1, 2), (−5, 6), (7, −4) and (k, −2) taken in order. If the area of the quadrilateral is zero, find the value of k.
Prove that the lines joining the middle points of the opposite sides of a quadrilateral and the join of the middle points of its diagonals meet in a point and bisect one another
If G be the centroid of a triangle ABC and P be any other point in the plane, prove that PA2+ PB2 + PC2 = GA2 + GB2 + GC2 + 3GP2.
If the coordinates of the mid-points of the sides of a triangle are (1, 1), (2, —3) and (3, 4), find the vertices of the triangle.
Find the area of a triangle whose sides are 9 cm, 12 cm and 15 cm ?
Show that the points A (3,1) , B (0,-2) , C(1,1) and D (4,4) are the vertices of parallelogram ABCD.
A(7, -3), B(5,3) and C(3,-1) are the vertices of a ΔABC and AD is its median. Prove that the median AD divides ΔABC into two triangles of equal areas.
Find the area of ΔABC with vertices A(0, -1), B(2,1) and C(0, 3). Also, find the area of the triangle formed by joining the midpoints of its sides. Show that the ratio of the areas of two triangles is 4:1.
If the centroid of ΔABC having vertices A (a,b) , B (b,c) and C (c,a) is the origin, then find the value of (a+b+c).
If the area of triangle ABC formed by A(x, y), B(1, 2) and C(2, 1) is 6 square units, then prove that x + y = 15 ?
What is the area of a triangle with base 4.8 cm and height 3.6 cm?
The table given below contains some measures of the right angled triangle. Find the unknown values.
| Base | Height | Area |
| ? | 12 m | 24 sq.m |
If Δ = `|(1, x, x^2),(1, y, y^2),(1, z, z^2)|`, Δ1 = `|(1, 1, 1),(yz, zx, xy),(x, y, z)|`, then prove that ∆ + ∆1 = 0.
Find the values of k if the points A(k + 1, 2k), B(3k, 2k + 3) and C(5k – 1, 5k) are collinear.
In the given figure, ratio of the area of triangle ABC to the area of triangle ACD is the same as the ratio of base BC of triangle ABC to the base CD of ΔACD.

Find the missing value:
| Base | Height | Area of Triangle |
| 22 cm | ______ | 170.5 cm2 |
