Advertisements
Advertisements
प्रश्न
Find the area of a triangle whose vertices are
(6,3), (-3,5) and (4,2)
उत्तर
We know area of triangle formed by three points (x1y1) , (x2y2), and (x3y3)is given by `triangle=1/2 [x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)]`
The vertices are given as (6, 3), (−3, 5), (4, −2).
`triangle=1/2[6(5+2)-3(-2-3)+4(3-5)]`
`=1/2 [6xx7-3xx(-5)+4xx(-2)]`
`=1/2[42+15-8]`
`49/2 `sq units
APPEARS IN
संबंधित प्रश्न
Find the values of k so that the area of the triangle with vertices (1, -1), (-4, 2k) and (-k, -5) is 24 sq. units.
Find the area of the following triangle:
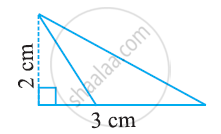
Prove that (2, -2) (-2, 1) and (5, 2) are the vertices of a right-angled triangle. Find the area of the triangle and the length of the hypotenuse.
If A(5,2), B(2, -2) and C(-2, t) are the vertices of a right triangle with ∠B=90° , then find the value of t .
Prove that the points A(2, 4), b(2, 6) and (2 +`sqrt(3)` ,5) are the vertices of an equilateral triangle
If A, B, C are the angles of a triangle, then ∆ = `|(sin^2"A", cot"A", 1),(sin^2"B", cot"B", 1),(sin^2"C", cot"C", 1)|` = ______.
The value of the determinant `abs((1,"x","x"^3),(1,"y","y"^3),(1,"z","z"^3))` is ____________.
The area of a triangle with vertices (a, b + c), (b, c + a) and (c, a + b) is ______.
Points A(–6, 10), B(–4, 6) and C(3, –8) are collinear such that AB = `2/9` AC.
Find the missing value:
| Base | Height | Area of Triangle |
| 22 cm | ______ | 170.5 cm2 |
