Advertisements
Advertisements
Question
Find the area of the quadrilaterals, the coordinates of whose vertices are
(1, 2), (6, 2), (5, 3) and (3, 4)
Solution
Let the vertices of the quadrilateral be A (1, 2), B (6, 2), C (5, 3), and D (3, 4). Join AC to form two triangles ΔABC and ΔACD.
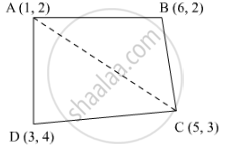
Area of a triangle `=1/2 {x_1(y_2-y_3)+x_2(y_3-y_1)+(y_1-y_2)}`
Area of ΔABC `=1/2 {1(2-3)+6(3-2+5(2-2)}`
`=1/2(-1+6)=5/2` square units
Area of ΔACD `=1/2{1(3-4)+5(4-2)+3(2-3)}`
`=1/2 {-1+10-3}=3` square units
Area of `square`ABCD = Area of ΔABC +Area of ΔACD
`=(5/2+3)` square units = 11/2 square units
APPEARS IN
RELATED QUESTIONS
Prove that the points (a, 0), (0, b) and (1, 1) are collinear if `1/a+1/b=1`
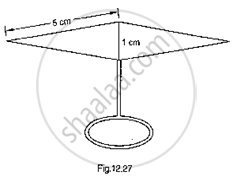
Find the area of the blades of thc magnetic compass shown in Fig.. 12.27. (Take √11 = 3.32).
Find the centroid of ΔABC whose vertices are A(-1, 0) B(5, -2) and C(8,2)
Show that the points A (3,1) , B (0,-2) , C(1,1) and D (4,4) are the vertices of parallelogram ABCD.
Find the value of k so that the area of the triangle with vertices A (k+1, 1), B(4, -3) and C(7, -k) is 6 square units
Find the value of x for which the points (x, −1), (2, 1) and (4, 5) are collinear ?
Using integration, find the area of triangle ABC, whose vertices are A(2, 5), B(4, 7) and C(6, 2).
If the points (3, -2), (x, 2), (8, 8) are collinear, then find the value of x.
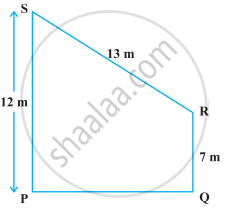
Find the area of the trapezium PQRS with height PQ given in the following figure.
Area of a right-angled triangle is 30 cm2. If its smallest side is 5 cm, then its hypotenuse is ______.
