Advertisements
Advertisements
प्रश्न
Find values of k if area of triangle is 4 square units and vertices are (−2, 0), (0, 4), (0, k)
उत्तर
Area of a triangle = `1/2 abs ((x_1,y_1,1),(x_2,y_2,1),(x_3,y_3,1))`
`=> 1/2 abs ((-2,0,1),(0,4,1),(0, k,1))`
`= 1/2 [-2 (4 - k) - 0 (0 - 0) + 1 (0 - 0)]`
`= 1/2 xx (-2) (4 - k)`
= k - 4
= `pm 4`
When, k - 4 = 4, `therefore k = 8`
k - 4 = 4 `therefore k = 0`
APPEARS IN
संबंधित प्रश्न
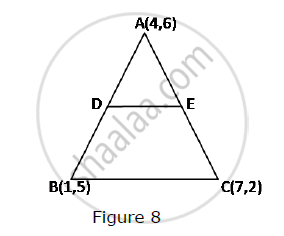
In Fig. 8, the vertices of ΔABC are A(4, 6), B(1, 5) and C(7, 2). A line-segment DE is drawn to intersect the sides AB and AC at D and E respectively such that `(AD)/(AB)=(AE)/(AC)=1/3 `Calculate th area of ADE and compare it with area of ΔABCe.
Prove that the area of a triangle with vertices (t, t −2), (t + 2, t + 2) and (t + 3, t) is independent of t.
For what value of x will the points (x, –1), (2, 1) and (4, 5) lie on a line ?
Find the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are (0, -1), (2, 1) and (0, 3). Find the ratio of this area to the area of the given triangle
median of a triangle divides it into two triangles of equal areas. Verify this result for ΔABC whose vertices are A (4, - 6), B (3, - 2) and C (5, 2).
Find the centre of a circle passing through the points (6, − 6), (3, − 7) and (3, 3).
The two opposite vertices of a square are (− 1, 2) and (3, 2). Find the coordinates of the other two vertices.
ABCD is a rectangle formed by the points A(-1, -1), B(-1, 4), C(5, 4) and D(5, -1). P, Q, R and S are the midpoints of AB, BC, CD and DA respectively. Is the quadrilateral PQRS a square? a rectangle? or a rhombus? Justify your answer.
Find the area of a triangle with vertices at the point given in the following:
(−2, −3), (3, 2), (−1, −8)
Find equation of line joining (1, 2) and (3, 6) using the determinant.
Find the area of the following triangle:

ΔABC is isosceles with AB = AC = 7.5 cm and BC = 9 cm (see the given figure). The height AD from A to BC, is 6 cm. Find the area of ΔABC. What will be the height from C to AB i.e., CE?

Show that the following sets of points are collinear.
(2, 5), (4, 6) and (8, 8)
Find the area of a triangle two sides of which are 18 cm and 10 cm and the perimeter is 42cm ?
In a ΔABC, AB = 15 cm, BC = 13 cm and AC = 14 cm. Find the area of ΔABC and hence its altitude on AC ?
Show that the points A(-5,6), B(3,0) and C(9,8) are the vertices of an isosceles right-angled triangle. Calculate its area.
Show that the points O(0,0), A`( 3,sqrt(3)) and B (3,-sqrt(3))` are the vertices of an equilateral triangle. Find the area of this triangle.
Find the third vertex of a ΔABC if two of its vertices are B(-3,1) and C (0,-2) and its centroid is at the origin
Find the area of ΔABC whose vertices are:
A(10,-6) , B (2,5) and C(-1,-3)
Find the value of k so that the area of the triangle with vertices A (k+1, 1), B(4, -3) and C(7, -k) is 6 square units
If the area of triangle ABC formed by A(x, y), B(1, 2) and C(2, 1) is 6 square units, then prove that x + y = 15 ?
If the points A (x, y), B (3, 6) and C (−3, 4) are collinear, show that x − 3y + 15 = 0.
Find BC, if the area of the triangle ABC is 36 cm2 and the height AD is 3 cm.

If the sides of a triangle are 3 cm, 4 cm and 5 cm, then the area is
The table given below contains some measures of the right angled triangle. Find the unknown values.
| Base | Height | Area |
| 20 cm | 40 cm | ? |
The value of the determinant `abs((1,"x","x"^3),(1,"y","y"^3),(1,"z","z"^3))` is ____________.
If the points (2, -3), (k, -1), and (0, 4) are collinear, then find the value of 4k.
The area of a triangle with vertices A(3, 0), B(7, 0) and C(8, 4) is ______.
Points A(3, 1), B(12, –2) and C(0, 2) cannot be the vertices of a triangle.
Find the area of the triangle whose vertices are (–8, 4), (–6, 6) and (–3, 9).
The area of ∆ABC is 8 cm2 in which AB = AC = 4 cm and ∠A = 90º.
Find the cost of laying grass in a triangular field of sides 50 m, 65 m and 65 m at the rate of Rs 7 per m2.
Area of triangle MNO in the figure is ______.
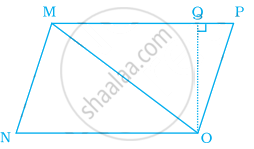
Triangles having the same base have equal area.
Let a vector `αhati + βhatj` be obtained by rotating the vector `sqrt(3)hati + hatj` by an angle 45° about the origin in counter-clockwise direction in the first quadrant. Then the area of triangle having vertices (α, β), (0, β) and (0, 0) is equal to ______.
If (a, b), (c, d) and (e, f) are the vertices of ΔABC and Δ denotes the area of ΔABC, then `|(a, c, e),(b, d, f),(1, 1, 1)|^2` is equal to ______.
Find the missing value:
| Base | Height | Area of Triangle |
| 22 cm | ______ | 170.5 cm2 |
