Advertisements
Advertisements
प्रश्न
ΔABC is isosceles with AB = AC = 7.5 cm and BC = 9 cm (see the given figure). The height AD from A to BC, is 6 cm. Find the area of ΔABC. What will be the height from C to AB i.e., CE?

उत्तर
Area of triangle ABC = `1/2 xx "Base" xx "Height"`
= `1/2 xx BC xx AD`
= `1/2 xx 9 xx 6`
= 27 cm2
Area of triangle ABC = `1/2 xx "Base" xx "Height"`
= `1/2 xx AB xx CE`
`27 = 1/2 xx 7.5 xx CE`
CE = `(27 xx 2)/7.5`
CE = 7.2 cm
APPEARS IN
संबंधित प्रश्न
median of a triangle divides it into two triangles of equal areas. Verify this result for ΔABC whose vertices are A (4, - 6), B (3, - 2) and C (5, 2).
Show that the following sets of points are collinear.
(1, −1), (2, 1) and (4, 5)
If the coordinates of the mid-points of the sides of a triangle are (1, 1), (2, —3) and (3, 4), find the vertices of the triangle.
Show that the points (-3, -3),(3,3) and C (-3 `sqrt(3) , 3 sqrt(3))` are the vertices of an equilateral triangle.
Find the area of ΔABC whose vertices are:
A(-5,7) , B (-4,-5) and C (4,5)
Let ∆ = `|("A"x, x^2, 1),("B"y, y^2, 1),("C"z, z^2, 1)|`and ∆1 = `|("A", "B", "C"),(x, y, z),(zy, zx, xy)|`, then ______.
The area of a triangle with vertices (a, b + c), (b, c + a) and (c, a + b) is ______.
Points A(–6, 10), B(–4, 6) and C(3, –8) are collinear such that AB = `2/9` AC.
Area of triangle PQR is 100 cm2 as shown in the below figure. If altitude QT is 10 cm, then its base PR is ______.

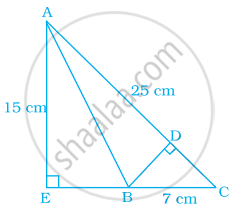
In the given figure, triangle AEC is right-angled at E, B is a point on EC, BD is the altitude of triangle ABC, AC = 25 cm, BC = 7 cm and AE = 15 cm. Find the area of triangle ABC and the length of DB.