Advertisements
Advertisements
प्रश्न
Let ∆ = `|("A"x, x^2, 1),("B"y, y^2, 1),("C"z, z^2, 1)|`and ∆1 = `|("A", "B", "C"),(x, y, z),(zy, zx, xy)|`, then ______.
पर्याय
∆1 = – ∆
∆ ≠ ∆1
∆ – ∆1 = 0
None of these
उत्तर
Let ∆ = `|("A"x, x^2, 1),("B"y, y^2, 1),("C"z, z^2, 1)|`and ∆1 = `|("A", "B", "C"),(x, y, z),(zy, zx, xy)|`, then ∆ – ∆1 = 0.
Explanation:
∆1 = `|("A", "B", "C"),(x, y, z),(zy, zx, xy)|`
= `|("A", x, yz),("B", y, zx),("C", z, xy)|`
= `1/(xyz) |("A"x, x^2, xyz),("B"y, y^2, xyz),("C"z, z^2, xyz)|`
= `(xyz)/(xyz)|("A"x, x^2, 1),("B"y, y^2, 1),("C"z, z^2, 1)|`
= ∆
APPEARS IN
संबंधित प्रश्न
If the points A(−1, −4), B(b, c) and C(5, −1) are collinear and 2b + c = 4, find the values of b and c.
Prove that the points (2, – 2), (–3, 8) and (–1, 4) are collinear
For what value of k are the points (k, 2 – 2k), (–k + 1, 2k) and (–4 – k, 6 – 2k) are collinear ?
The two opposite vertices of a square are (− 1, 2) and (3, 2). Find the coordinates of the other two vertices.
Show that points A (a, b + c), B (b, c + a), C (c, a + b) are collinear.
Find values of k if area of triangle is 4 square units and vertices are (−2, 0), (0, 4), (0, k)
The area of a triangle is 5 sq units. Two of its vertices are (2, 1) and (3, –2). If the third vertex is (`7/2`, y). Find the value of y
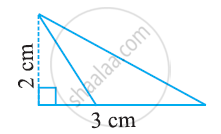
Find the area of the following triangle:
Show that the following sets of points are collinear.
(1, −1), (2, 1) and (4, 5)
The point A divides the join of P (−5, 1) and Q(3, 5) in the ratio k:1. Find the two values of k for which the area of ΔABC where B is (1, 5) and C(7, −2) is equal to 2 units.
Find the angle subtended at the origin by the line segment whose end points are (0, 100) and (10, 0).
If the coordinates of the mid-points of the sides of a triangle are (1, 1), (2, —3) and (3, 4), find the vertices of the triangle.
Show that the points A (3,1) , B (0,-2) , C(1,1) and D (4,4) are the vertices of parallelogram ABCD.
A(6,1) , B(8,2) and C(9,4) are the vertices of a parallelogram ABCD. If E is the midpoint of DC, find the area of ΔADE
Find the value of k so that the area of the triangle with vertices A (k+1, 1), B(4, -3) and C(7, -k) is 6 square units
Find the value of y for which the points A(-3, 9), B(2,y) and C(4,-5) are collinear.
For what values of k are the points A(8, 1) B(3, -2k) and C(k, -5) collinear.
Prove that the points A (a,0), B( 0,b) and C (1,1) are collinear, if `( 1/a+1/b) =1`.
Find the area of ΔABC with vertices A(0, -1), B(2,1) and C(0, 3). Also, find the area of the triangle formed by joining the midpoints of its sides. Show that the ratio of the areas of two triangles is 4:1.
Find the value of x for which the points (x, −1), (2, 1) and (4, 5) are collinear ?
Using integration, find the area of triangle ABC, whose vertices are A(2, 5), B(4, 7) and C(6, 2).
In ∆PQR, PR = 8 cm, QR = 4 cm and PL = 5 cm. 
Find:
(i) the area of the ∆PQR
(ii) QM.
The table given below contains some measures of the right angled triangle. Find the unknown values.
| Base | Height | Area |
| ? | 12 m | 24 sq.m |
If the co-ordinates of the vertices of an equilateral triangle with sides of length ‘a’ are (x1, y1), (x2, y2), (x3, y3), then `|(x_1, y_1, 1),(x_2, y_2, 1),(x_3, y_3, 1)|^2 = (3"a"^4)/4`
Show that the points (a + 5, a – 4), (a – 2, a + 3) and (a, a) do not lie on a straight line for any value of a.
The value of the determinant `abs((1,"x","x"^3),(1,"y","y"^3),(1,"z","z"^3))` is ____________.
If the points (3, -2), (x, 2), (8, 8) are collinear, then find the value of x.
The points (1,1), (-2, 7) and (3, -3) are ______.
A(6, 1), B(8, 2) and C(9, 4) are three vertices of a parallelogram ABCD. If E is the midpoint of DC, find the area of ∆ADE.
