Advertisements
Advertisements
प्रश्न
Find the value of x for which the points (x, −1), (2, 1) and (4, 5) are collinear ?
उत्तर
The points (x1, y1), (x2, y2) and (x3, y3) are collinear if `x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)`= 0 i.e., the area of triangle formed by the given points is zero.
Let the given points be A (x, − 1), B (2, 1) and C (4, 5).
The points A (x, − 1), B (2, 1) and C (4, 5) are collinear.
Therefore, Area of ΔABC = 0
`rArrx(1-5)+2[5-(-1)]+4(-1-1)=0`
`rArrx-4x+12-8=0`
`rArrx-4x+4=0`
`rArrx=1`
Thus, the value of x is 1.
APPEARS IN
संबंधित प्रश्न
Find the area of the triangle PQR with Q(3,2) and the mid-points of the sides through Q being (2,−1) and (1,2).
Find the centre of a circle passing through the points (6, − 6), (3, − 7) and (3, 3).
Show that points A (a, b + c), B (b, c + a), C (c, a + b) are collinear.
Find the area of the following triangle:

Find the area of the quadrilaterals, the coordinates of whose vertices are
(1, 2), (6, 2), (5, 3) and (3, 4)
Find the area of a triangle whose sides are respectively 150 cm, 120 cm and 200 cm ?
If G(-2, 1) is the centroid of a ΔABC and two of its vertices are A(1, -6) and B(-5, 2) , find the third vertex of the triangle.
Find the third vertex of a ΔABC if two of its vertices are B(-3,1) and C (0,-2) and its centroid is at the origin
In the given figure, if PR = 12 cm, QR = 6 cm and PL = 8 cm, then QM is ______.

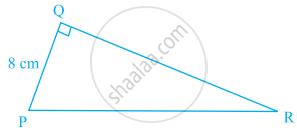
Area of a triangle PQR right-angled at Q is 60 cm2 in the figure. If the smallest side is 8 cm long, find the length of the other two sides.