Advertisements
Advertisements
प्रश्न
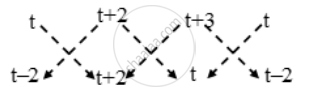
Prove that the area of a triangle with vertices (t, t −2), (t + 2, t + 2) and (t + 3, t) is independent of t.
उत्तर १
Let A(t, t − 2), B(t + 2, t + 2) and C(t + 2, t) be the vertices of the given triangle.
We know that the area of the triangle having vertices (x1, y1), (x2, y2) and (x3, y3) is
`1/2|x_1(y_2-y_3)+x^2(y_3-y_1)+x_3(y_1-y_2)||`
∴ Area of ∆ABC = `|1/2[x_1(y_2-y_3)+x^2(y_3-y_1)+x_3(y_1-y_2)||`
`=|1/2[t(t+2−t)+(t+2)(t−t+2)+(t+3)(t−2−t−2)]|`
`|1/2(2t+2t+4−4t−12)|`
`|-4|`
=4 square units
Hence, the area of the triangle with given vertices is independent of t.
उत्तर २
`therefore `
`rArr `
`rArr`
`rArr`
⇒ Area of ∆ABC = 4 sq. units
Hence, Area of ∆ABC is independent of t.
APPEARS IN
संबंधित प्रश्न
Find the values of k for which the points A(k + 1, 2k), B(3k, 2k + 3) and (5k – 1, 5k) are collinear.
If A(−4, 8), B(−3, −4), C(0, −5) and D(5, 6) are the vertices of a quadrilateral ABCD, find its area.
Find the area of a triangle with vertices at the point given in the following:
(1, 0), (6, 0), (4, 3)
Show that the following sets of points are collinear.
(2, 5), (4, 6) and (8, 8)
The point A divides the join of P (−5, 1) and Q(3, 5) in the ratio k:1. Find the two values of k for which the area of ΔABC where B is (1, 5) and C(7, −2) is equal to 2 units.
Show that the points O(0,0), A`( 3,sqrt(3)) and B (3,-sqrt(3))` are the vertices of an equilateral triangle. Find the area of this triangle.
Find a relation between x and y, if the points A(2, 1), B(x, y) and C(7,5) are collinear.
The area of a trapezium is 475 cm2 and the height is 19 cm. Find the lengths of its two parallel sides if one side is 4 cm greater than the other.
Let a vector `αhati + βhatj` be obtained by rotating the vector `sqrt(3)hati + hatj` by an angle 45° about the origin in counter-clockwise direction in the first quadrant. Then the area of triangle having vertices (α, β), (0, β) and (0, 0) is equal to ______.
Using determinants, find the area of ΔPQR with vertices P(3, 1), Q(9, 3) and R(5, 7). Also, find the equation of line PQ using determinants.
