Advertisements
Advertisements
प्रश्न
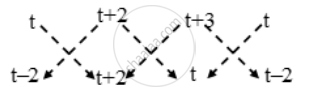
Prove that the area of a triangle with vertices (t, t −2), (t + 2, t + 2) and (t + 3, t) is independent of t.
उत्तर १
Let A(t, t − 2), B(t + 2, t + 2) and C(t + 2, t) be the vertices of the given triangle.
We know that the area of the triangle having vertices (x1, y1), (x2, y2) and (x3, y3) is
`1/2|x_1(y_2-y_3)+x^2(y_3-y_1)+x_3(y_1-y_2)||`
∴ Area of ∆ABC = `|1/2[x_1(y_2-y_3)+x^2(y_3-y_1)+x_3(y_1-y_2)||`
`=|1/2[t(t+2−t)+(t+2)(t−t+2)+(t+3)(t−2−t−2)]|`
`|1/2(2t+2t+4−4t−12)|`
`|-4|`
=4 square units
Hence, the area of the triangle with given vertices is independent of t.
उत्तर २
`therefore `
`rArr `
`rArr`
`rArr`
⇒ Area of ∆ABC = 4 sq. units
Hence, Area of ∆ABC is independent of t.
APPEARS IN
संबंधित प्रश्न
Find the area of the triangle ABC with A(1, −4) and mid-points of sides through A being (2, −1) and (0, −1).
If A(−4, 8), B(−3, −4), C(0, −5) and D(5, 6) are the vertices of a quadrilateral ABCD, find its area.
If A(4, –6), B(3, –2) and C(5, 2) are the vertices of ∆ABC, then verify the fact that a median of a triangle ABC divides it into two triangle of equal areas.
In each of the following find the value of 'k', for which the points are collinear.
(8, 1), (k, -4), (2, -5)
If the coordinates of the mid-points of the sides of a triangle are (3, 4) (4, 6) and (5, 7), find its vertices.
Show that the points O(0,0), A`( 3,sqrt(3)) and B (3,-sqrt(3))` are the vertices of an equilateral triangle. Find the area of this triangle.
The coordinates of the point P dividing the line segment joining the points A (1, 3) and B (4, 6) in the ratio 2 : 1 are:
In a triangle ABC, if `|(1, 1, 1),(1 + sin"A", 1 + sin"B", 1 + sin"C"),(sin"A" + sin^2"A", sin"B" + sin^2"B", sin"C" + sin^2"C")|` = 0, then prove that ∆ABC is an isoceles triangle.
Observe all the four triangles FAB, EAB, DAB and CAB as shown in the given figure.

- All triangles have the same base and the same altitude.
- All triangles are congruent.
- All triangles are equal in area.
- All triangles may not have the same perimeter.
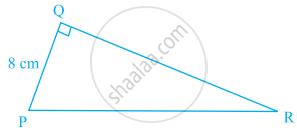
Area of a triangle PQR right-angled at Q is 60 cm2 in the figure. If the smallest side is 8 cm long, find the length of the other two sides.