Advertisements
Advertisements
प्रश्न
Show that the points O(0,0), A`( 3,sqrt(3)) and B (3,-sqrt(3))` are the vertices of an equilateral triangle. Find the area of this triangle.
उत्तर
The given points are O(0,0), A`( 3,sqrt(3)) and B (3,-sqrt(3))` .
`OA = sqrt((3-0)^2 +{ (sqrt(3)) -0}^2) = sqrt((3)^2 +(sqrt(3))^2) = sqrt(9+3) = sqrt(12) = 2sqrt(3) `units
`AB = sqrt((3-3)^2 +(-sqrt(3)-sqrt(3))^2) = sqrt((0) + (2 sqrt(3))^2) = sqrt(4(3)) = sqrt(12) =2sqrt(3)` units
`OB = sqrt((3-0)^2 + (-sqrt(3) -0)^2) = sqrt((3)^2 +(sqrt(3)^2) = sqrt(9+3) = sqrt(12) = 2 sqrt(3)` units
Therefore, `OA =AB = OB = 2 sqrt(3) ` units
Thus, the points O(0,0), A`( 3,sqrt(3)) and B (3,-sqrt(3))` are the vertices of an equilateral triangle Also, the area of the triangle `OAB = sqrt(3)/4 xx (" side")^2`
`=sqrt(3)/4 xx(2 sqrt(3) )^2`
`= sqrt(3)/4 xx 12`
`= 3 sqrt(3) ` square units
APPEARS IN
संबंधित प्रश्न
Find the values of k so that the area of the triangle with vertices (1, -1), (-4, 2k) and (-k, -5) is 24 sq. units.
Find the area of the triangle ABC with A(1, −4) and mid-points of sides through A being (2, −1) and (0, −1).
Find the area of the following triangle:
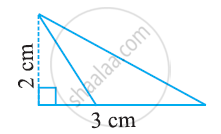
Show that the following sets of points are collinear.
(2, 5), (4, 6) and (8, 8)
If the coordinates of the mid-points of the sides of a triangle are (3, 4) (4, 6) and (5, 7), find its vertices.
Find the area of a triangle whose sides are respectively 150 cm, 120 cm and 200 cm ?
Show that the following points are collinear:
A(-5,1), B(5, 5) and C(10, 7)
For what value of x are the points A(-3, 12), B(7, 6) and C(x, 9) collinear.
A rectangular plot is given for constructing a house, having a measurement of 40 m long and 15 m in the front. According to the laws, a minimum of 3 m, wide space should be left in the front and back each and 2 m wide space on each of other sides. Find the largest area where house can be constructed.
Find the missing value:
| Base | Height | Area of parallelogram |
| ______ | 8.4 cm | 48.72 cm2 |
