Advertisements
Advertisements
प्रश्न
A thief runs with a uniform speed of 100 m/minute. After one minute, a policeman runs after the thief to catch him. He goes with a speed of 100 m/minute in the first minute and increases his speed by 10 m/minute every succeeding minute. After how many minutes the policeman will catch the thief.
उत्तर
Suppose the policeman catches the thief after t minutes.
Uniform speed of the thief = 100 metres/minute
∴ Distance covered by thief in (t + 1) minutes = 100 metres/minute × (t + 1) minutes = 100 (t + 1) metres
Distance covered by policeman in t minutes = Sum of t terms of an AP with first term 100 and common difference 10
=`t/2`[2×100+(t−1)×10] m
=t[100+5(t−1)]
=t(5t+95)
=5t2+95t
When the policeman catches the thief,
5t2+95t=100(t+1)
⇒5t2+95t=100t+100
⇒5t2−5t−100=0
⇒t2−t−20=0
⇒ t = − 4 and t = 5
∴ t = 5 (As t cannot be negative)
Thus, the policeman catches the thief after 5 minutes.
APPEARS IN
संबंधित प्रश्न
Solve the following system of equations by the method of cross-multiplication `\frac{x}{a}+\frac{y}{b}=a+b ; \frac{x}{a^{2}}+\frac{y}{b^{2}}=2`
For which value of k will the following pair of linear equations have no solution?
3x + y = 1
(2k – 1)x + (k – 1)y = 2k + 1
Form the pair of linear equations in the following problems and find their solutions (if they exist) by any algebraic method
Yash scored 40 marks in a test, getting 3 marks for each right answer and losing 1 mark for each wrong answer. Had 4 marks been awarded for each correct answer and 2 marks been deducted for each incorrect answer, then Yash would have scored 50 marks. How many questions were there in the test?
Solve the following systems of equations:
`x + y/2 = 4`
`x/3 + 2y = 5`
Solve each of the following systems of equations by the method of cross-multiplication :
`5/(x + y) - 2/(x - y) = -1`
`15/(x + y) + 7/(x - y) = 10`
where `x != 0 and y != 0`
Solve the system of equations by using the method of cross multiplication:
`(ax)/b- (by)/a – (a + b) = 0, ax – by – 2ab = 0`
Solve the system of equations by using the method of cross multiplication:
`a/x - b/y = 0, (ab^2)/x + (a^2b)/y = (a^2 + b^2), where x ≠ 0 and y ≠ 0.`
Find the values of x and y in the following rectangle [see figure].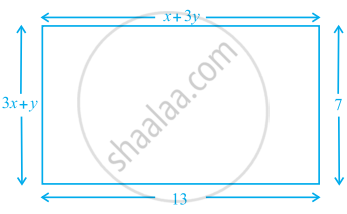
Ankita travels 14 km to her home partly by rickshaw and partly by bus. She takes half an hour if she travels 2 km by rickshaw, and the remaining distance by bus. On the other hand, if she travels 4 km by rickshaw and the remaining distance by bus, she takes 9 minutes longer. Find the speed of the rickshaw and of the bus.
Anuj had some chocolates, and he divided them into two lots A and B. He sold the first lot at the rate of ₹ 2 for 3 chocolates and the second lot at the rate of ₹ 1 per chocolate, and got a total of ₹ 400. If he had sold the first lot at the rate of ₹ 1 per chocolate, and the second lot at the rate of ₹4 for 5 chocolates, his total collection would have been ₹460. Find the total number of chocolates he had.
