Advertisements
Advertisements
प्रश्न
Solve the system of equations by using the method of cross multiplication:
`(ax)/b- (by)/a – (a + b) = 0, ax – by – 2ab = 0`
उत्तर
The given equations may be written as:
`(ax)/b - (by)/a – (a + b) = 0 ` ……(i)
ax – by – 2ab = 0 ……(ii)
Here, `a_1 = a/b, b_1 = (−b)/a, c_1 = -(a + b), a_2 = a, b_2 = -b and c_2 = -2ab`
By cross multiplication, we have:
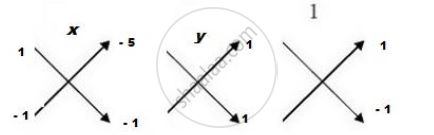
`∴ x/[(−b/a)×(−2ab) −(−b) ×(−(a+b)]) = y/([−(a+b) × a −(−2ab) × a/b)] = 1/([a/b ×(−b)−a ×(−b/a)])`
`⇒x/(2b^2−b(a+b)) = y/(−a(a+b)+2a^2) = 1/(−a+b)`
`⇒x/(2b^2−ab− b^2 ) = y/(−a^2 −ab+2a^2) = 1/(−a+b)`
`⇒x/(b^2−ab) = y/(a^2 −ab) = 1/(−(a−b))`
`⇒x/(−b(a−b)) = y/(a(a−b)) = 1/(−(a−b))`
`⇒ x = (−b(a−b))/(−(a−b)) = b, y = (a(a−b))/(−(a−a)) = -a`
Hence, x = b and y = -a is the required solution.
APPEARS IN
संबंधित प्रश्न
Solve the follownig system of equations by the method of cross-multiplication.
2x – 6y + 10 = 0
3x – 7y + 13 = 0
Which of the following pairs of linear equations has unique solution, no solution or infinitely many solutions? In case there is a unique solution, find it by using cross multiplication method
2x + y = 5
3x + 2y = 8
For which value of k will the following pair of linear equations have no solution?
3x + y = 1
(2k – 1)x + (k – 1)y = 2k + 1
Solve the following systems of equations:
`x + 2y = 3/2`
`2x + y = 3/2`
Solve each of the following systems of equations by the method of cross-multiplication :
2x + y = 35
3x + 4y = 65
Solve each of the following systems of equations by the method of cross-multiplication
2x − y = 6
x − y = 2
Solve the system of equations by using the method of cross multiplication:
2x + y – 35 = 0,
3x + 4y – 65 = 0
Determine, algebraically, the vertices of the triangle formed by the lines
3x – y = 2
2x – 3y = 2
x + 2y = 8
A shopkeeper sells a saree at 8% profit and a sweater at 10% discount, thereby, getting a sum Rs 1008. If she had sold the saree at 10% profit and the sweater at 8% discount, she would have got Rs 1028. Find the cost price of the saree and the list price (price before discount) of the sweater.
Susan invested certain amount of money in two schemes A and B, which offer interest at the rate of 8% per annum and 9% per annum, respectively. She received Rs 1860 as annual interest. However, had she interchanged the amount of investments in the two schemes, she would have received Rs 20 more as annual interest. How much money did she invest in each scheme?
