Advertisements
Advertisements
प्रश्न
Solve the system of equations by using the method of cross multiplication:
2ax + 3by – (a + 2b) = 0,
3ax + 2by – (2a + b) = 0
उत्तर
The given equations may be written as:
2ax + 3by – (a + 2b) = 0 ……(i)
3ax + 2by – (2a + b) = 0 ……(ii)
Here, `a_1 =2a, b_1 =3b, c_1 = -(a + 2b), a_2 = 3a, b_2 = 2b and c_2 = -(2a + b)`
By cross multiplication, we have
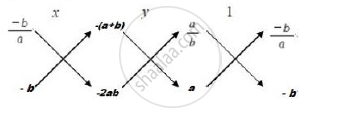
`∴ x/([3b ×(−(2a+ b) −2b) ×(−(a+2b))]) = y/([−(a+2b) × 3a −2a ×(−(2a+b))]) = 1/([2a ×2b −3a ×3b])`
`⇒x/((−6ab−3b^2+2ab+4b^2)) = y/((−3a^2−6ab+4a^2+2ab)) = 1/(4ab−9ab)`
`⇒x/(b^2−4ab) = y/(a^2 −4ab) = 1/(−5ab)`
`⇒ x/(−b(4a−b)) = y/(−a(4b−a)) = 1/(−5ab)`
`⇒x = (−b(4a−b))/(−5ab )= ((4a−b))/(5a,) y = (−a(4b−a))/(−5ab) = ((4b−a))/(5b)`
Hence, x = `((4a−b))/(5a) and y = ((4b−a))/(5b)` is the required solution.
APPEARS IN
संबंधित प्रश्न
Solve the following system of equations by the method of cross-multiplication `\frac{x}{a}+\frac{y}{b}=a+b ; \frac{x}{a^{2}}+\frac{y}{b^{2}}=2`
Which of the following pairs of linear equations has unique solution, no solution, or infinitely many solutions. In case there is a unique solution, find it by using cross multiplication method
x – 3y – 3 = 0
3x – 9y – 2 = 0
For which values of a and b does the following pair of linear equations have an infinite number of solutions?
2x + 3y = 7
(a – b) x + (a + b) y = 3a + b – 2
Form the pair of linear equations in the following problems and find their solutions (if they exist) by any algebraic method
Yash scored 40 marks in a test, getting 3 marks for each right answer and losing 1 mark for each wrong answer. Had 4 marks been awarded for each correct answer and 2 marks been deducted for each incorrect answer, then Yash would have scored 50 marks. How many questions were there in the test?
Solve the following systems of equations:
`x + y/2 = 4`
`x/3 + 2y = 5`
Solve each of the following systems of equations by the method of cross-multiplication :
`a^2/x - b^2/y = 0`
`(a^2b)/x + (b^2a)/y = a + b, x , y != 0`
Solve the following pair of equations:
`x/a + y/b = a + b, x/a^2 + y/b^2 = 2, a, b ≠ 0`
Ankita travels 14 km to her home partly by rickshaw and partly by bus. She takes half an hour if she travels 2 km by rickshaw, and the remaining distance by bus. On the other hand, if she travels 4 km by rickshaw and the remaining distance by bus, she takes 9 minutes longer. Find the speed of the rickshaw and of the bus.
A railway half ticket costs half the full fare, but the reservation charges are the same on a half ticket as on a full ticket. One reserved first class ticket from the station A to B costs Rs 2530. Also, one reserved first class ticket and one reserved first class half ticket from A to B costs Rs 3810. Find the full first class fare from station A to B, and also the reservation charges for a ticket.
A shopkeeper sells a saree at 8% profit and a sweater at 10% discount, thereby, getting a sum Rs 1008. If she had sold the saree at 10% profit and the sweater at 8% discount, she would have got Rs 1028. Find the cost price of the saree and the list price (price before discount) of the sweater.
