Advertisements
Advertisements
प्रश्न
Solve the system of equations by using the method of cross multiplication:
2ax + 3by – (a + 2b) = 0,
3ax + 2by – (2a + b) = 0
उत्तर
The given equations may be written as:
2ax + 3by – (a + 2b) = 0 ……(i)
3ax + 2by – (2a + b) = 0 ……(ii)
Here, `a_1 =2a, b_1 =3b, c_1 = -(a + 2b), a_2 = 3a, b_2 = 2b and c_2 = -(2a + b)`
By cross multiplication, we have
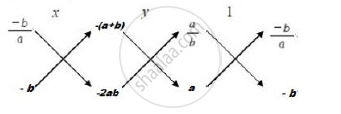
`∴ x/([3b ×(−(2a+ b) −2b) ×(−(a+2b))]) = y/([−(a+2b) × 3a −2a ×(−(2a+b))]) = 1/([2a ×2b −3a ×3b])`
`⇒x/((−6ab−3b^2+2ab+4b^2)) = y/((−3a^2−6ab+4a^2+2ab)) = 1/(4ab−9ab)`
`⇒x/(b^2−4ab) = y/(a^2 −4ab) = 1/(−5ab)`
`⇒ x/(−b(4a−b)) = y/(−a(4b−a)) = 1/(−5ab)`
`⇒x = (−b(4a−b))/(−5ab )= ((4a−b))/(5a,) y = (−a(4b−a))/(−5ab) = ((4b−a))/(5b)`
Hence, x = `((4a−b))/(5a) and y = ((4b−a))/(5b)` is the required solution.
APPEARS IN
संबंधित प्रश्न
A motorboat whose speed in still water is 18 km/h, takes 1 hour more to go 24 km upstream than to return downstream to the same spot. Find the speed of the stream.
Solve the following systems of equations:
4u + 3y = 8
`6u - 4y = -5`
Solve the following systems of equations:
`10/(x + y) + 2/(x - y) = 4`
`15/(x + y) - 5/(x - y) = -2`
Solve each of the following systems of equations by the method of cross-multiplication
2x − y = 6
x − y = 2
Solve each of the following systems of equations by the method of cross-multiplication
`x/a + y/b = 2`
`ax - by = a^2 - b^2`
Solve each of the following systems of equations by the method of cross-multiplication
`(a - b)x + (a + b)y = 2a^2 - 2b^2`
(a + b)(a + y) = 4ab
Solve the system of equations by using the method of cross multiplication:
7x - 2y – 3 = 0,
`11x - 3/2 y – 8 = 0.`
Solve the following pair of equations:
`1/(2x) - 1/y = -1, 1/x + 1/(2y) = 8, x, y ≠ 0`
Solve the following pair of equations:
`x/a + y/b = a + b, x/a^2 + y/b^2 = 2, a, b ≠ 0`
A motor boat can travel 30 km upstream and 28 km downstream in 7 hours. It can travel 21 km upstream and return in 5 hours. Find the speed of the boat in still water and the speed of the stream.
