Question

Solve the system of equations by using the method of cross multiplication:
`(ax)/b- (by)/a – (a + b) = 0, ax – by – 2ab = 0`

Answer 1

The given equations may be written as:
`(ax)/b - (by)/a – (a + b) = 0  `               ……(i)
ax – by – 2ab = 0                                 ……(ii)
Here, `a_1 = a/b, b_1 = (−b)/a, c_1 = -(a + b), a_2 = a, b_2 = -b and c_2 = -2ab`
By cross multiplication, we have:

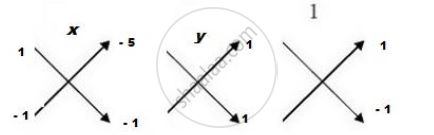
`∴ x/[(−b/a)×(−2ab) −(−b) ×(−(a+b)]) = y/([−(a+b) × a −(−2ab) × a/b)] = 1/([a/b ×(−b)−a ×(−b/a)])`
`⇒x/(2b^2−b(a+b))  = y/(−a(a+b)+2a^2) = 1/(−a+b)`
`⇒x/(2b^2−ab− b^2 ) = y/(−a^2 −ab+2a^2) = 1/(−a+b)`
`⇒x/(b^2−ab) = y/(a^2 −ab) = 1/(−(a−b))`
`⇒x/(−b(a−b)) = y/(a(a−b)) = 1/(−(a−b))`
`⇒ x = (−b(a−b))/(−(a−b)) = b, y = (a(a−b))/(−(a−a)) = -a`
Hence, x = b and y = -a is the required solution.