Advertisements
Advertisements
Question
Solve the system of equations by using the method of cross multiplication:
`(ax)/b- (by)/a – (a + b) = 0, ax – by – 2ab = 0`
Solution
The given equations may be written as:
`(ax)/b - (by)/a – (a + b) = 0 ` ……(i)
ax – by – 2ab = 0 ……(ii)
Here, `a_1 = a/b, b_1 = (−b)/a, c_1 = -(a + b), a_2 = a, b_2 = -b and c_2 = -2ab`
By cross multiplication, we have:
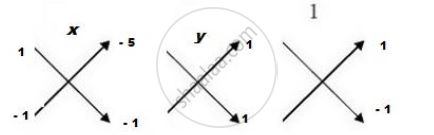
`∴ x/[(−b/a)×(−2ab) −(−b) ×(−(a+b)]) = y/([−(a+b) × a −(−2ab) × a/b)] = 1/([a/b ×(−b)−a ×(−b/a)])`
`⇒x/(2b^2−b(a+b)) = y/(−a(a+b)+2a^2) = 1/(−a+b)`
`⇒x/(2b^2−ab− b^2 ) = y/(−a^2 −ab+2a^2) = 1/(−a+b)`
`⇒x/(b^2−ab) = y/(a^2 −ab) = 1/(−(a−b))`
`⇒x/(−b(a−b)) = y/(a(a−b)) = 1/(−(a−b))`
`⇒ x = (−b(a−b))/(−(a−b)) = b, y = (a(a−b))/(−(a−a)) = -a`
Hence, x = b and y = -a is the required solution.
APPEARS IN
RELATED QUESTIONS
Solve the following system of equations in x and y by cross-multiplication method
`(a – b) x + (a + b) y = a^2 – 2ab – b^2`
`(a + b) (x + y) = a^2 + b^2`
Solve the following system of equations by the method of cross-multiplication. `\frac{a}{x}-\frac{b}{y}=0;\text{}\frac{ab^{2}}{x}+\frac{a^{2}b}{y}=a^{2}+b^{2};` Where x ≠ 0, y ≠ 0
Form the pair of linear equations in the following problems and find their solutions (if they exist) by any algebraic method
Yash scored 40 marks in a test, getting 3 marks for each right answer and losing 1 mark for each wrong answer. Had 4 marks been awarded for each correct answer and 2 marks been deducted for each incorrect answer, then Yash would have scored 50 marks. How many questions were there in the test?
Solve the following systems of equations:
`1/(2x) + 1/(3y) = 2`
`1/(3x) + 1/(2y) = 13/6`
Solve each of the following systems of equations by the method of cross-multiplication
ax + by = a − b
bx − ay = a + b
Solve each of the following systems of equations by the method of cross-multiplication
5ax + 6by = 28
3ax + 4by = 18
Solve the system of equations by using the method of cross multiplication:
6x - 5y - 16 = 0,
7x - 13y + 10 = 0
Solve the system of equations by using the method of cross multiplication:
`a/x - b/y = 0, (ab^2)/x + (a^2b)/y = (a^2 + b^2), where x ≠ 0 and y ≠ 0.`
A father's age is three times the sum of the ages of his two children. After 5 years his age will be two times the sum of their ages. Find the present age of the father.
Solve the following pair of equations:
`x/3 + y/4 = 4, (5x)/6 - y/4 = 4`
