Question

Solve the system of equations by using the method of cross multiplication:
`a/x - b/y = 0, (ab^2)/x + (a^2b)/y = (a^2 + b^2), where x ≠ 0 and y ≠ 0.`

Answer 1

Substituting `1/x = u and 1/y` = v in the given equations, we get
au – bv + 0 = 0                                       …….(i)
`ab^2u + a^2bv – (a^2 + b^2) = 0`                   ……(ii)
Here,` a_1 =a, b_1 = -b, c_1 = 0, a_2 = ab^2, b_2 = a^2b and c_2 = -( a^2 + b^2).`
So, by cross-multiplication, we have

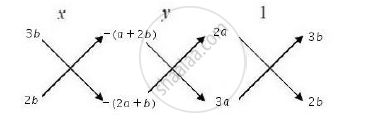
`u/(b_1c_2− b_2c_1) = v/(c_1a_2− c_2a_1) = 1/(a_1b_2− a_2b_1)`
`⇒u/((−b)[−(a^2+b^2)]−(a^2b)(0)) = v/((0)(ab^2)−(−a^2−b^2)(a)) = 1/((a)(a^2b)−(ab^2)(−b))`
`⇒u/(b(a^2+b^2)) = v/(a(a^2 + b^2) )= 1/(ab(a^2 + b^2))`
`⇒u= (b(a^2+b^2))/(ab(a^2 + b^2)) , v = (a(a^2 + b^2))/(ab(a^2 + b^2))`
`⇒u = 1/a, v= 1/b`
`⇒1/x = 1/a, 1/y = 1/b`
⇒x = a, y = b
Hence, x = a and y = b.