Advertisements
Advertisements
प्रश्न
Solve the system of equations by using the method of cross multiplication:
`a/x - b/y = 0, (ab^2)/x + (a^2b)/y = (a^2 + b^2), where x ≠ 0 and y ≠ 0.`
उत्तर
Substituting `1/x = u and 1/y` = v in the given equations, we get
au – bv + 0 = 0 …….(i)
`ab^2u + a^2bv – (a^2 + b^2) = 0` ……(ii)
Here,` a_1 =a, b_1 = -b, c_1 = 0, a_2 = ab^2, b_2 = a^2b and c_2 = -( a^2 + b^2).`
So, by cross-multiplication, we have
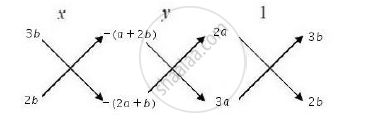
`u/(b_1c_2− b_2c_1) = v/(c_1a_2− c_2a_1) = 1/(a_1b_2− a_2b_1)`
`⇒u/((−b)[−(a^2+b^2)]−(a^2b)(0)) = v/((0)(ab^2)−(−a^2−b^2)(a)) = 1/((a)(a^2b)−(ab^2)(−b))`
`⇒u/(b(a^2+b^2)) = v/(a(a^2 + b^2) )= 1/(ab(a^2 + b^2))`
`⇒u= (b(a^2+b^2))/(ab(a^2 + b^2)) , v = (a(a^2 + b^2))/(ab(a^2 + b^2))`
`⇒u = 1/a, v= 1/b`
`⇒1/x = 1/a, 1/y = 1/b`
⇒x = a, y = b
Hence, x = a and y = b.
APPEARS IN
संबंधित प्रश्न
A thief runs with a uniform speed of 100 m/minute. After one minute, a policeman runs after the thief to catch him. He goes with a speed of 100 m/minute in the first minute and increases his speed by 10 m/minute every succeeding minute. After how many minutes the policeman will catch the thief.
Which of the following pairs of linear equations has unique solution, no solution, or infinitely many solutions. In case there is a unique solution, find it by using cross multiplication method
3x – 5y = 20
6x – 10y = 40
Solve the following systems of equations:
`4/x + 3y = 14`
`3/x - 4y = 23`
Solve the following systems of equations:
`(7x - 2y)/"xy" = 5`
`(8x + 7y)/"xy" = 15`
Solve each of the following systems of equations by the method of cross-multiplication :
x + 2y + 1 = 0
2x − 3y − 12 = 0
Solve each of the following systems of equations by the method of cross-multiplication :
`2/x + 3/y = 13`
`5/4 - 4/y = -2`
where `x != 0 and y != 0`
Solve each of the following systems of equations by the method of cross-multiplication :
6(ax + by) = 3a + 2b
6(bx - ay) = 3b - 2a
Solve the system of equations by using the method of cross multiplication:
2x + 5y – 1 = 0, 2x + 3y – 3 = 0
Solve the system of equations by using the method of cross multiplication:
2ax + 3by – (a + 2b) = 0,
3ax + 2by – (2a + b) = 0
If `|( 4,5), (m , 3)|` = 22, then find the value of m.
