Question

Solve the system of equation by using the method of cross multiplication:
`5/("x+y") - 2/("x− y") + 1 = 0, 15/("x+y") + 7/("x− y") – 10 = 0`

Answer 1

Taking `1/(x+y) = u and 1/(x− y)` = v, the given equations become:
5u - 2v + 1 = 0                                …..(i)
15u + 7v – 10 = 0                           ……(ii)
Here, `a_1 = 5, b_1 = -2, c_1 = 1, a_2 = 15, b_2 = -7 and c_2 = -10`
By cross multiplication, we have:

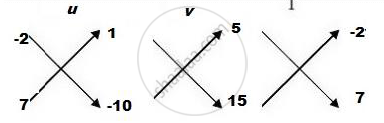
`∴ u/([−2×(−10) −1 ×7] )= v/([1 × 15 −(−10) ×5]) = 1/([35+30])`
`⇒u/((20−7)) = v/((15+50)) = 1/65`
`⇒u/13 = v/65 = 1/65`
`⇒u = 13/65 = 1/5, v = 65/65 = 1`
`⇒ 1/(x+y) = 1/5, 1/(x−y) = 1`
So, (x + y) = 5                  …….(iii)
and (x – y) = 1                  ……(iv)
Again, the above equations (ii) and (iv) may be written as:
x + y – 5 = 0                       …..(i)
x – y – 1 = 0                      ……(ii)
Here, `a_1 = 1, b_1 = 1, c_1 = -5, a_2 = 1, b_2 = -1 and c_2 = -1`
By cross multiplication, we have:

`∴ x/([1×(−1) −(−5) ×(−1)]) = y/([(−5) × 1 −(−1) ×1]) = 1/([1 ×(−1)−1 ×1])`
`⇒x/((−1−5)) = y/((−5+1)) = 1/((−1−1))`
`⇒x/(−6 )= v/(−4) = 1/(−2)`
`⇒x = (−6)/(−2) = 3, y = (−4)/(−2) = 2`
Hence, x = 3 and y = 2 is the required solution.