Advertisements
Advertisements
प्रश्न
Solve the system of equation by using the method of cross multiplication:
`5/("x+y") - 2/("x− y") + 1 = 0, 15/("x+y") + 7/("x− y") – 10 = 0`
उत्तर
Taking `1/(x+y) = u and 1/(x− y)` = v, the given equations become:
5u - 2v + 1 = 0 …..(i)
15u + 7v – 10 = 0 ……(ii)
Here, `a_1 = 5, b_1 = -2, c_1 = 1, a_2 = 15, b_2 = -7 and c_2 = -10`
By cross multiplication, we have:
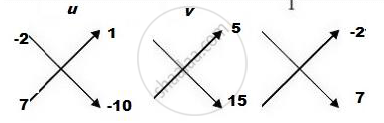
`∴ u/([−2×(−10) −1 ×7] )= v/([1 × 15 −(−10) ×5]) = 1/([35+30])`
`⇒u/((20−7)) = v/((15+50)) = 1/65`
`⇒u/13 = v/65 = 1/65`
`⇒u = 13/65 = 1/5, v = 65/65 = 1`
`⇒ 1/(x+y) = 1/5, 1/(x−y) = 1`
So, (x + y) = 5 …….(iii)
and (x – y) = 1 ……(iv)
Again, the above equations (ii) and (iv) may be written as:
x + y – 5 = 0 …..(i)
x – y – 1 = 0 ……(ii)
Here, `a_1 = 1, b_1 = 1, c_1 = -5, a_2 = 1, b_2 = -1 and c_2 = -1`
By cross multiplication, we have:

`∴ x/([1×(−1) −(−5) ×(−1)]) = y/([(−5) × 1 −(−1) ×1]) = 1/([1 ×(−1)−1 ×1])`
`⇒x/((−1−5)) = y/((−5+1)) = 1/((−1−1))`
`⇒x/(−6 )= v/(−4) = 1/(−2)`
`⇒x = (−6)/(−2) = 3, y = (−4)/(−2) = 2`
Hence, x = 3 and y = 2 is the required solution.
APPEARS IN
संबंधित प्रश्न
Solve the following system of equations by the method of cross-multiplication. `\frac{a}{x}-\frac{b}{y}=0;\text{}\frac{ab^{2}}{x}+\frac{a^{2}b}{y}=a^{2}+b^{2};` Where x ≠ 0, y ≠ 0
Which of the following pairs of linear equations has unique solution, no solution, or infinitely many solutions. In case there is a unique solution, find it by using cross multiplication method
x – 3y – 3 = 0
3x – 9y – 2 = 0
Which of the following pairs of linear equations has unique solution, no solution, or infinitely many solutions. In case there is a unique solution, find it by using cross multiplication method
3x – 5y = 20
6x – 10y = 40
For which values of a and b does the following pair of linear equations have an infinite number of solutions?
2x + 3y = 7
(a – b) x + (a + b) y = 3a + b – 2
Solve the following pair of linear equations by the substitution and cross-multiplication methods
8x + 5y = 9
3x + 2y = 4
Solve the following systems of equations:
4u + 3y = 8
`6u - 4y = -5`
Solve the following systems of equations:
`x + y/2 = 4`
`x/3 + 2y = 5`
Solve the following systems of equations:
`4/x + 3y = 14`
`3/x - 4y = 23`
Solve each of the following systems of equations by the method of cross-multiplication :
(a + 2b)x + (2a − b)y = 2
(a − 2b)x + (2a + b)y = 3
Solve each of the following systems of equations by the method of cross-multiplication :
`(ax)/b - (by)/a = a + b`
ax - by = 2ab
