Advertisements
Advertisements
प्रश्न
Solve the system of equations by using the method of cross multiplication:
`1/x + 1/y = 7, 2/x + 3/y = 17`
उत्तर
Taking `1/x = u and 1/y` = v, the given equations become:
u + v = 7
2u + 3v = 17
The given equations may be written as:
u + v – 7 = 0 …..(i)
2u + 3v – 17 = 0 ……(ii)
Here, `a_1 = 1, b_1 = 1, c_1 = -7, a_2 = 2, b_2 = 3 and c_2 = -17`
By cross multiplication, we have:
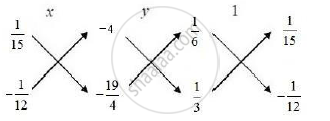
`∴ u/([1×(−17) −3 ×(−7)]) = v/([(−7) × 2 −1 ×(−17)] )= 1/([3−2])`
`⇒u/((−17+21) )= v/((−14+17)) = 1/(1)`
`⇒u/4 = v/3 = 1/1`
`⇒u = 4/1 = 4, v = 3/1 = 3`
`⇒ 1/x = 4, 1/y = 3`
`⇒ x = 1/4, y = 1/3`
Hence, x = `1/4 and y = 1/3` is the required solution.
APPEARS IN
संबंधित प्रश्न
A thief runs with a uniform speed of 100 m/minute. After one minute, a policeman runs after the thief to catch him. He goes with a speed of 100 m/minute in the first minute and increases his speed by 10 m/minute every succeeding minute. After how many minutes the policeman will catch the thief.
Form the pair of linear equations in the following problems and find their solutions (if they exist) by any algebraic method:
A fraction becomes `1/3` when 1 is subtracted from the numerator and it becomes `1/4` when 8 is added to its denominator. Find the fraction.
Form the pair of linear equations in the following problems and find their solutions (if they exist) by any algebraic method
The area of a rectangle gets reduced by 9 square units, if its length is reduced by 5 units and breadth is increased by 3 units. If we increase the length by 3 units and the breadth by 2 units, the area increases by 67 square units. Find the dimensions of the rectangle.
Solve the following systems of equations:
`1/(2x) + 1/(3y) = 2`
`1/(3x) + 1/(2y) = 13/6`
Solve each of the following systems of equations by the method of cross-multiplication :
`x(a - b + (ab)/(a - b)) = y(a + b - (ab)/(a + b))`
`x + y = 2a^2`
Solve each of the following systems of equations by the method of cross-multiplication :
mx – my = m2 + n2
x + y = 2m
Solve the system of equations by using the method of cross multiplication:
`(ax)/b- (by)/a – (a + b) = 0, ax – by – 2ab = 0`
Solve 0.4x + 0.3y = 1.7; 0.7 x − 0.2y = 0.8
Find the values of x and y in the following rectangle [see figure].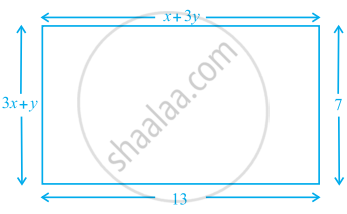
Solve the following pair of equations:
`x/a + y/b = a + b, x/a^2 + y/b^2 = 2, a, b ≠ 0`
