Advertisements
Advertisements
प्रश्न
Solve the system of equations by using the method of cross multiplication:
`1/x + 1/y = 7, 2/x + 3/y = 17`
उत्तर
Taking `1/x = u and 1/y` = v, the given equations become:
u + v = 7
2u + 3v = 17
The given equations may be written as:
u + v – 7 = 0 …..(i)
2u + 3v – 17 = 0 ……(ii)
Here, `a_1 = 1, b_1 = 1, c_1 = -7, a_2 = 2, b_2 = 3 and c_2 = -17`
By cross multiplication, we have:
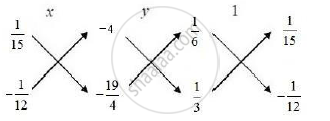
`∴ u/([1×(−17) −3 ×(−7)]) = v/([(−7) × 2 −1 ×(−17)] )= 1/([3−2])`
`⇒u/((−17+21) )= v/((−14+17)) = 1/(1)`
`⇒u/4 = v/3 = 1/1`
`⇒u = 4/1 = 4, v = 3/1 = 3`
`⇒ 1/x = 4, 1/y = 3`
`⇒ x = 1/4, y = 1/3`
Hence, x = `1/4 and y = 1/3` is the required solution.
APPEARS IN
संबंधित प्रश्न
Solve the following system of equations by cross-multiplication method.
ax + by = a – b; bx – ay = a + b
Which of the following pairs of linear equations has unique solution, no solution, or infinitely many solutions. In case there is a unique solution, find it by using cross multiplication method
3x – 5y = 20
6x – 10y = 40
Solve the following systems of equations:
4u + 3y = 8
`6u - 4y = -5`
Solve each of the following systems of equations by the method of cross-multiplication
x + ay = b
ax − by = c
Solve each of the following systems of equations by the method of cross-multiplication :
mx – my = m2 + n2
x + y = 2m
Solve the system of equations by using the method of cross multiplication:
6x - 5y - 16 = 0,
7x - 13y + 10 = 0
Solve the system of equations by using the method of cross multiplication:
3x + 2y + 25 = 0, 2x + y + 10 = 0
Complete the activity to find the value of x.
3x + 2y = 11 …(i) and 2x + 3y = 4 …(ii)
Solution:
Multiply equation (i) by _______ and equation (ii) by _______.
`square` × (3x + 2y = 11) ∴ 9x + 6y = 33 …(iii)
`square` × (2x + 3y = 4) ∴ 4x + 6y = 8 …(iv)
Subtract (iv) from (iii),
`square` x = 25
∴ x = `square`
Ankita travels 14 km to her home partly by rickshaw and partly by bus. She takes half an hour if she travels 2 km by rickshaw, and the remaining distance by bus. On the other hand, if she travels 4 km by rickshaw and the remaining distance by bus, she takes 9 minutes longer. Find the speed of the rickshaw and of the bus.
A two-digit number is obtained by either multiplying the sum of the digits by 8 and then subtracting 5 or by multiplying the difference of the digits by 16 and then adding 3. Find the number.
