Advertisements
Advertisements
प्रश्न
Solve each of the following systems of equations by the method of cross-multiplication :
mx – my = m2 + n2
x + y = 2m
उत्तर
The given system of equations may be written as
`mx - ny - (m^2 + n^2) = 0`
`x + y - 2m = 0
Here
`a_1 = m, b_1 = -n, c_1 = -(n^2 + n^2)`
`a_2 = 1, b_2 = 1, c_2 = -2m`
By cross multiplication, we have
`x/(2mn + (m^2 + n^2)) = (-y)/(-2m^2 + (m^2 + n^2)) = 1/(m + n)`
`=> x/(2mn + m^2 + n^2) = (-y)/(-m^2 + n^2) = 1/(m + n)`
`=> x/(m + n)^2 = (-y)/(-m^2 + n^2) = 1/(m + n)`
Now
`x/(m + n)^2 = 1/(m + n)`
`=> x = (m + n^2)/(m + n)`
=> x = m + n
And
`(-y)/(-m^2 + n^2) = 1/(m + n)`
`=> -y = (-m^2 + n^2)/(n + n)`
`=> y = (m^2 - n^2)/(m + n)`
`=> y = ((m - n)(m + n))/(m + n)`
=> y = m - n
Hence, x = m + n, y = m - n is the solution of the given system of equation.
APPEARS IN
संबंधित प्रश्न
Solve the following system of equations by cross-multiplication method x + y = a – b; ax – by = a2 + b2
Solve the following system of equations by cross-multiplications method.
`a(x + y) + b (x – y) = a^2 – ab + b^2`
`a(x + y) – b (x – y) = a^2 + ab + b^2`
Form the pair of linear equations in the following problems and find their solutions (if they exist) by any algebraic met
Places A and B are 100 km apart on a highway. One car starts from A and another from B at the same time. If the cars travel in the same direction at different speeds, they meet in 5 hours. If they travel towards each other, they meet in 1 hour. What are the speeds of the two cars?
Solve the following systems of equations:
4u + 3y = 8
`6u - 4y = -5`
Solve each of the following systems of equations by the method of cross-multiplication :
`5/(x + y) - 2/(x - y) = -1`
`15/(x + y) + 7/(x - y) = 10`
where `x != 0 and y != 0`
Solve each of the following systems of equations by the method of cross-multiplication :
`(ax)/b - (by)/a = a + b`
ax - by = 2ab
Find the values of x and y in the following rectangle [see figure].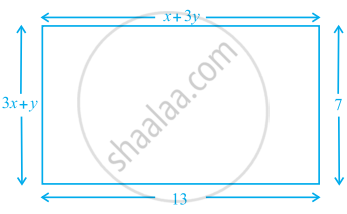
Solve the following pair of equations:
`(2xy)/(x + y) = 3/2, (xy)/(2x - y) = (-3)/10, x + y ≠ 0, 2x - y ≠ 0`
Find the solution of the pair of equations `x/10 + y/5 - 1` = 0 and `x/8 + y/6` = 15. Hence, find λ, if y = λx + 5.
For what values of k will the following pair of linear equations have infinitely many solutions?
kx + 3y – (k – 3) = 0
12x + ky – k = 0
