Advertisements
Advertisements
प्रश्न
Find the values of x and y in the following rectangle [see figure].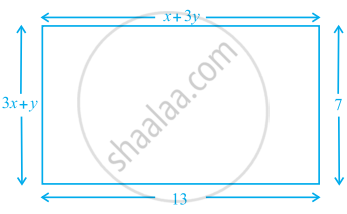
उत्तर
Using property of rectangle,
We know that,
Lengths are equal,
i.e., CD = AB
Hence, x + 3y = 13 ......(i)
Breadth are equal,
i.e., AD = BC
Hence, 3x + y = 7 ......(ii)
On multiplying equation (ii) by 3 and then subtracting equation (i), we get
9x + 3y = 21
x + 3y = 13
– – –
8x = 8
So, x = 1
On substituting x = 1 in equation (i), we get
3y = 12
y = 4
Therefore, the required values of x and y are 1 and 4, respectively.
APPEARS IN
संबंधित प्रश्न
Solve the following system of equations by cross-multiplications method.
`a(x + y) + b (x – y) = a^2 – ab + b^2`
`a(x + y) – b (x – y) = a^2 + ab + b^2`
Solve the following systems of equations:
`x/3 + y/4 =11`
`(5x)/6 - y/3 = -7`
Solve the following systems of equations:
`3x - (y + 7)/11 + 2 = 10`
`2y + (x + 10)/7 = 10`
Solve the following systems of equations:
`1/(2x) + 1/(3y) = 2`
`1/(3x) + 1/(2y) = 13/6`
Solve each of the following systems of equations by the method of cross-multiplication
ax + by = a2
bx + ay = b2
Solve each of the following systems of equations by the method of cross-multiplication
`x/a + y/b = a + b`
Solve each of the following systems of equations by the method of cross-multiplication :
`x(a - b + (ab)/(a - b)) = y(a + b - (ab)/(a + b))`
`x + y = 2a^2`
Solve each of the following systems of equations by the method of cross-multiplication
`(a - b)x + (a + b)y = 2a^2 - 2b^2`
(a + b)(a + y) = 4ab
Solve each of the following systems of equations by the method of cross-multiplication :
2(ax – by) + a + 4b = 0
2(bx + ay) + b – 4a = 0
Solve the system of equations by using the method of cross multiplication:
3x - 2y + 3 = 0,
4x + 3y – 47 = 0
