Advertisements
Advertisements
Question
Find the values of x and y in the following rectangle [see figure].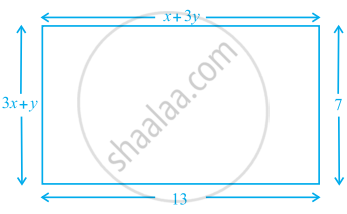
Solution
Using property of rectangle,
We know that,
Lengths are equal,
i.e., CD = AB
Hence, x + 3y = 13 ......(i)
Breadth are equal,
i.e., AD = BC
Hence, 3x + y = 7 ......(ii)
On multiplying equation (ii) by 3 and then subtracting equation (i), we get
9x + 3y = 21
x + 3y = 13
– – –
8x = 8
So, x = 1
On substituting x = 1 in equation (i), we get
3y = 12
y = 4
Therefore, the required values of x and y are 1 and 4, respectively.
APPEARS IN
RELATED QUESTIONS
Solve the following system of equations in x and y by cross-multiplication method
`(a – b) x + (a + b) y = a^2 – 2ab – b^2`
`(a + b) (x + y) = a^2 + b^2`
Form the pair of linear equations in the following problems and find their solutions (if they exist) by any algebraic method :
A part of monthly hostel charges is fixed and the remaining depends on the number of days one has taken food in the mess. When a student A takes food for 20 days she has to pay Rs 1000 as hostel charges whereas a student B, who takes food for 26 days, pays Rs 1180 as hostel charges. Find the fixed charges and the cost of food per day.
Solve the following systems of equations:
`x/3 + y/4 =11`
`(5x)/6 - y/3 = -7`
Solve the following systems of equations:
`(7x - 2y)/"xy" = 5`
`(8x + 7y)/"xy" = 15`
Solve each of the following systems of equations by the method of cross-multiplication
x + ay = b
ax − by = c
Solve each of the following systems of equations by the method of cross-multiplication
ax + by = a2
bx + ay = b2
Solve each of the following systems of equations by the method of cross-multiplication :
2ax + 3by = a + 2b
3ax + 2by = 2a + b
Solve each of the following systems of equations by the method of cross-multiplication :
(a + 2b)x + (2a − b)y = 2
(a − 2b)x + (2a + b)y = 3
Solve the system of equations by using the method of cross multiplication:
3x + 2y + 25 = 0, 2x + y + 10 = 0
Solve 0.4x + 0.3y = 1.7; 0.7 x − 0.2y = 0.8
