Advertisements
Advertisements
Question
Solve the system of equations by using the method of cross multiplication:
3x + 2y + 25 = 0, 2x + y + 10 = 0
Solution
The given equations are:
3x + 2y + 25 = 0 …….(i)
2x + y + 10 = 0 …….(ii)
Here `a_1 = 3, b_1 = 2, c_1 = 25, a_2 = 2, b_2 = 1 and c_2 = 10`
By cross multiplication, we have:
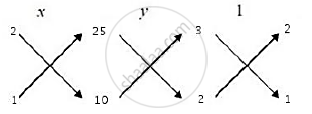 \
\
`∴ x/([2×10 −25 × 1]) = y/([25 × 2 −10 × 3] )= 1/([3 × 1−2 × 2])`
`⇒x/((20−25)) = y/((50−30) )= 1/((3−4))`
`⇒x/((−5)) = y/20 = 1/((−1))`
`⇒x = (−5)/(−1) = 5, y = 20/((−1)) = -20`
Hence, x = 5 and y = -20 is the required solution.
APPEARS IN
RELATED QUESTIONS
Solve the following system of equations by the method of cross-multiplication `\frac{x}{a}+\frac{y}{b}=a+b ; \frac{x}{a^{2}}+\frac{y}{b^{2}}=2`
Solve the following systems of equations:
`1/(2x) + 1/(3y) = 2`
`1/(3x) + 1/(2y) = 13/6`
Solve each of the following systems of equations by the method of cross-multiplication :
x + 2y + 1 = 0
2x − 3y − 12 = 0
Solve each of the following systems of equations by the method of cross-multiplication :
`ax + by = (a + b)/2`
3x + 5y = 4
Solve each of the following systems of equations by the method of cross-multiplication :
mx – my = m2 + n2
x + y = 2m
Solve each of the following systems of equations by the method of cross-multiplication :
`(ax)/b - (by)/a = a + b`
ax - by = 2ab
Solve the system of equations by using the method of cross multiplication:
6x - 5y - 16 = 0,
7x - 13y + 10 = 0
Solve the system of equations by using the method of cross multiplication:
2ax + 3by – (a + 2b) = 0,
3ax + 2by – (2a + b) = 0
Solve the following pair of equations:
`x/a + y/b = a + b, x/a^2 + y/b^2 = 2, a, b ≠ 0`
In a competitive examination, one mark is awarded for each correct answer while `1/2` mark is deducted for every wrong answer. Jayanti answered 120 questions and got 90 marks. How many questions did she answer correctly?
