Advertisements
Advertisements
प्रश्न
Solve the system of equations by using the method of cross multiplication:
3x + 2y + 25 = 0, 2x + y + 10 = 0
उत्तर
The given equations are:
3x + 2y + 25 = 0 …….(i)
2x + y + 10 = 0 …….(ii)
Here `a_1 = 3, b_1 = 2, c_1 = 25, a_2 = 2, b_2 = 1 and c_2 = 10`
By cross multiplication, we have:
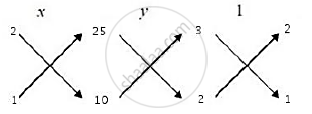 \
\
`∴ x/([2×10 −25 × 1]) = y/([25 × 2 −10 × 3] )= 1/([3 × 1−2 × 2])`
`⇒x/((20−25)) = y/((50−30) )= 1/((3−4))`
`⇒x/((−5)) = y/20 = 1/((−1))`
`⇒x = (−5)/(−1) = 5, y = 20/((−1)) = -20`
Hence, x = 5 and y = -20 is the required solution.
APPEARS IN
संबंधित प्रश्न
Solve the following system of equations by the method of cross-multiplication.
11x + 15y = – 23; 7x – 2y = 20
Which of the following pairs of linear equations has unique solution, no solution, or infinitely many solutions. In case there is a unique solution, find it by using cross multiplication method
3x – 5y = 20
6x – 10y = 40
Solve the following systems of equations:
`x + 2y = 3/2`
`2x + y = 3/2`
Solve the following systems of equations:
0.5x + 0.7y = 0.74
0.3x + 0.5y = 0.5
Solve the system of equations by using the method of cross multiplication:
`(ax)/b- (by)/a – (a + b) = 0, ax – by – 2ab = 0`
Complete the activity to find the value of x.
3x + 2y = 11 …(i) and 2x + 3y = 4 …(ii)
Solution:
Multiply equation (i) by _______ and equation (ii) by _______.
`square` × (3x + 2y = 11) ∴ 9x + 6y = 33 …(iii)
`square` × (2x + 3y = 4) ∴ 4x + 6y = 8 …(iv)
Subtract (iv) from (iii),
`square` x = 25
∴ x = `square`
Solve the following pair of equations:
`x/3 + y/4 = 4, (5x)/6 - y/4 = 4`
A railway half ticket costs half the full fare, but the reservation charges are the same on a half ticket as on a full ticket. One reserved first class ticket from the station A to B costs Rs 2530. Also, one reserved first class ticket and one reserved first class half ticket from A to B costs Rs 3810. Find the full first class fare from station A to B, and also the reservation charges for a ticket.
Susan invested certain amount of money in two schemes A and B, which offer interest at the rate of 8% per annum and 9% per annum, respectively. She received Rs 1860 as annual interest. However, had she interchanged the amount of investments in the two schemes, she would have received Rs 20 more as annual interest. How much money did she invest in each scheme?
For what values of k will the following pair of linear equations have infinitely many solutions?
kx + 3y – (k – 3) = 0
12x + ky – k = 0
