Advertisements
Advertisements
Question
Solve the system of equations by using the method of cross multiplication:
2x + 5y – 1 = 0, 2x + 3y – 3 = 0
Solution
The given equations may be written as:
2x + 5y – 1 = 0 …….(i)
2x + 3y – 3 = 0 …….(ii)
Here a1 = 2, b1 = 5, c1 = -1, a2 = 2, b2 = 3 and c2 = -3
By cross multiplication, we have:
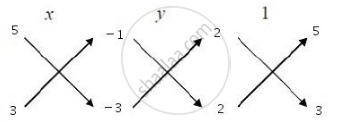
`∴ x/([5×(−3) −3 ×(−1)] )= y/([(−1) × 2 −(−3) × 2]) = 1/([2 × 3−2 × 5])`
`⇒x/((−15+3))= y/((−2+6) )= 1/((6−10))`
`⇒x/(−12) = y/4 = 1/(−4)`
`⇒x = (−12)/(−4 )= 3, y = 4/(−4 )= -1`
Hence, x = 3 and y = -1 is the required solution.
APPEARS IN
RELATED QUESTIONS
Solve the following system of equations by cross-multiplication method.
ax + by = a – b; bx – ay = a + b
Solve the following system of equations by cross-multiplication method ax + by = 1; `bx + ay = \frac{(a+b)^{2}}{a^{2}+b^{2}-1`
Which of the following pairs of linear equations has unique solution, no solution, or infinitely many solutions. In case there is a unique solution, find it by using cross multiplication method
x – 3y – 3 = 0
3x – 9y – 2 = 0
Which of the following pairs of linear equations has unique solution, no solution, or infinitely many solutions. In case there is a unique solution, find it by using cross multiplication method.
x – 3y – 7 = 0
3x – 3y – 15 = 0
Solve the following systems of equations:
0.5x + 0.7y = 0.74
0.3x + 0.5y = 0.5
Solve each of the following systems of equations by the method of cross-multiplication
ax + by = a − b
bx − ay = a + b
Solve each of the following systems of equations by the method of cross-multiplication
bx + cy = a + b
`ax (1/(a - b) - 1/(a + b)) + cy(1/(b -a) - 1/(b + a)) = (2a)/(a + b)`
A motor boat can travel 30 km upstream and 28 km downstream in 7 hours. It can travel 21 km upstream and return in 5 hours. Find the speed of the boat in still water and the speed of the stream.
Vijay had some bananas, and he divided them into two lots A and B. He sold the first lot at the rate of Rs 2 for 3 bananas and the second lot at the rate of Re 1 per banana, and got a total of Rs 400. If he had sold the first lot at the rate of Re 1 per banana, and the second lot at the rate of Rs 4 for 5 bananas, his total collection would have been Rs 460. Find the total number of bananas he had.
For what values of k will the following pair of linear equations have infinitely many solutions?
kx + 3y – (k – 3) = 0
12x + ky – k = 0
