Advertisements
Advertisements
Question
Solve each of the following systems of equations by the method of cross-multiplication
ax + by = a − b
bx − ay = a + b
Solution
The given system of equations is
ax + by = a − b .....(i)
bx − ay = a + b ....(ii)
here
`a_1 - a, b_1 = b, c_1 = b - a`
`a_2 = b, b_2 = -a, c_2 = -a-b`
By cross multiplication, we get
`=> x/((-a-b)xx(b)-(b-a)xx(-a)) = (-y)/((-a-b)xx(a)-(b-a)xx(-b)) = 1/(-axxa-bxxb)`
`=> x/(-ab -b^2 + ab -a^2) = (-y)/(-a^2-ab-b^2 + ab)= 1/(-a^2 - b^2)`
`=> x/(-b^2 - a^2) = (-y)/(=a^2 - b^2) = 1/(-a^2 - b^2)`
Now
`x/(-b^2-a^2) = 1/(-a^2-b^2)`
`=> x = (-b^2 - a^2)/(-a^2 - b^2)`
`=(-(b^2 + a^2))/(a^2 + b^2)`
`= (a^2 + b^2)/(a^2 + b^2)`
=> x= 1
`(-y)/(-a^2 -b^2) = 1/(-a^2-b^2)`
`=> -y = (-(a^2 + b^2))/(-(a^2 + b^2))`
=> -y = 1
=> y = -1
Hence x = 1, y = -1 is the solution of the given system of the equations
APPEARS IN
RELATED QUESTIONS
Which of the following pairs of linear equations has unique solution, no solution or infinitely many solutions? In case there is a unique solution, find it by using cross multiplication method
2x + y = 5
3x + 2y = 8
Which of the following pairs of linear equations has unique solution, no solution, or infinitely many solutions. In case there is a unique solution, find it by using cross multiplication method.
x – 3y – 7 = 0
3x – 3y – 15 = 0
For which value of k will the following pair of linear equations have no solution?
3x + y = 1
(2k – 1)x + (k – 1)y = 2k + 1
Solve the following systems of equations:
`x + 2y = 3/2`
`2x + y = 3/2`
Solve each of the following systems of equations by the method of cross-multiplication
3x + 2y + 25 = 0
2x + y + 10 = 0
Solve each of the following systems of equations by the method of cross-multiplication
`(x + y)/(xy) = 2`
`(x - y)/(xy) = 6`
Solve the system of equations by using the method of cross multiplication:
`(ax)/b- (by)/a – (a + b) = 0, ax – by – 2ab = 0`
Solve the system of equations by using the method of cross multiplication:
2ax + 3by – (a + 2b) = 0,
3ax + 2by – (2a + b) = 0
Find the values of x and y in the following rectangle [see figure].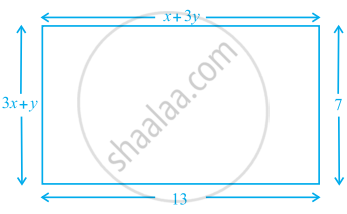
Solve the following pair of equations:
`x/a + y/b = a + b, x/a^2 + y/b^2 = 2, a, b ≠ 0`
