Advertisements
Advertisements
Question
Solve the system of equations by using the method of cross multiplication:
6x - 5y - 16 = 0,
7x - 13y + 10 = 0
Solution
The given equations are:
6x - 5y - 16 = 0 …….(i)
7x - 13y + 10 = 0 …….(ii)
Here `a_1 = 6, b_1 = -5, c_1 = -16, a_2 = 7, b_2 = -13 and c_2 = 10`
By cross multiplication, we have:
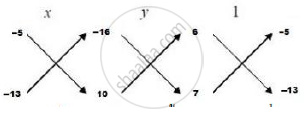
∴ `x/([(−5)×10 −(−16) ×(−13)]) = y/([(−16)×7 −10 × 6]) = 1/([6 ×(−13)−(−5) × 7])`
`⇒x/((−50−208)) = y/((−112−60)) = 1/((−78+35))`
`⇒x/(−258) = y/((−172)) = 1/((43))`
`⇒x = (−258)/(−43) = 6, y = (−172)/(−43) = 4`
Hence, x = 6 and y = 4 is the required solution.
APPEARS IN
RELATED QUESTIONS
A train travels at a certain average speed for a distance of 54 km and then travels a distance of 63 km at an average speed of 6 km/h more than the first speed. If it takes 3 hours to complete the total journey, what is its first speed?
Solve the follownig system of equations by the method of cross-multiplication.
2x – 6y + 10 = 0
3x – 7y + 13 = 0
Which of the following pairs of linear equations has unique solution, no solution or infinitely many solutions? In case there is a unique solution, find it by using cross multiplication method
2x + y = 5
3x + 2y = 8
Form the pair of linear equations in the following problems and find their solutions (if they exist) by any algebraic method
The area of a rectangle gets reduced by 9 square units, if its length is reduced by 5 units and breadth is increased by 3 units. If we increase the length by 3 units and the breadth by 2 units, the area increases by 67 square units. Find the dimensions of the rectangle.
Solve the following systems of equations:
`x + y/2 = 4`
`x/3 + 2y = 5`
Solve the following systems of equations:
`sqrt2x + sqrt3y = 0`
`sqrt3x - sqrt8y = 0`
Solve each of the following systems of equations by the method of cross-multiplication
ax + by = a2
bx + ay = b2
Solve each of the following systems of equations by the method of cross-multiplication
bx + cy = a + b
`ax (1/(a - b) - 1/(a + b)) + cy(1/(b -a) - 1/(b + a)) = (2a)/(a + b)`
Solve each of the following systems of equations by the method of cross-multiplication :
`(ax)/b - (by)/a = a + b`
ax - by = 2ab
Complete the activity to find the value of x.
3x + 2y = 11 …(i) and 2x + 3y = 4 …(ii)
Solution:
Multiply equation (i) by _______ and equation (ii) by _______.
`square` × (3x + 2y = 11) ∴ 9x + 6y = 33 …(iii)
`square` × (2x + 3y = 4) ∴ 4x + 6y = 8 …(iv)
Subtract (iv) from (iii),
`square` x = 25
∴ x = `square`
