Advertisements
Advertisements
Question
A train travels at a certain average speed for a distance of 54 km and then travels a distance of 63 km at an average speed of 6 km/h more than the first speed. If it takes 3 hours to complete the total journey, what is its first speed?
Solution
Let x be the first speed of the train.
We know that `t=3 hours` Thus,we have,
`54/x+63/(x+6)=3 hours`
`54(x+6)+63x/(x(x+6))=3`
`54(x+6)+63x=3(x(x+6))`
`54x+324+63x=3x^2+18x`
`117x+324=3x^2+18x`
`3x^2-117x-324+18x=0`
`3x^2-99x-324=0`
`x^3-33x-108=0`
`x(x-36)+3(x-36)=0`
`(x+3)(x-36)=0`
`(x+3)=0 or (x-36)=0`
`x=-3 " or " x=36`
Speed cannot be negative and hence intial speed of the train is 36 km/hour.
APPEARS IN
RELATED QUESTIONS
Solve the following system of equations by cross-multiplication method.
2x + 3y + 8 = 0
4x + 5y + 14 = 0
Solve the following system of equations by the method of cross-multiplication.
11x + 15y = – 23; 7x – 2y = 20
Solve the following system of equations by cross-multiplication method ax + by = 1; `bx + ay = \frac{(a+b)^{2}}{a^{2}+b^{2}-1`
Which of the following pairs of linear equations has unique solution, no solution, or infinitely many solutions. In case there is a unique solution, find it by using cross multiplication method
3x – 5y = 20
6x – 10y = 40
Solve each of the following systems of equations by the method of cross-multiplication :
mx – my = m2 + n2
x + y = 2m
Solve the system of equation by using the method of cross multiplication:
`5/("x+y") - 2/("x− y") + 1 = 0, 15/("x+y") + 7/("x− y") – 10 = 0`
A father's age is three times the sum of the ages of his two children. After 5 years his age will be two times the sum of their ages. Find the present age of the father.
Find the values of x and y in the following rectangle [see figure].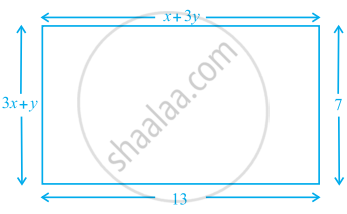
Solve the following pair of equations:
43x + 67y = – 24, 67x + 43y = 24
A person, rowing at the rate of 5 km/h in still water, takes thrice as much time in going 40 km upstream as in going 40 km downstream. Find the speed of the stream.
