Advertisements
Advertisements
Question
Solve the system of equations by using the method of cross multiplication:
3x - 2y + 3 = 0,
4x + 3y – 47 = 0
Solution
The given equations are:
3x - 2y + 3 = 0 …….(i)
4x + 3y – 47 = 0 …….(ii)
Here` a_1 = 3, b_1 = -2, c_1 = 3, a_2 = 4, b_2 = 3 and c_2 = -47`
By cross multiplication, we have:
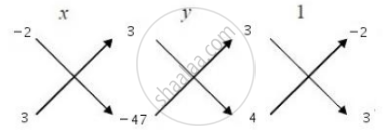
∴ `x/([(−2)×(−47)−3 × 3]) = y/[(3 ×4 −(−47)× 3]) = 1/([3 ×3 −(−2) × 4])`
`⇒x/((94−9)) = y/((12+141) )= 1/((9+8))`
`⇒x/((85)) = y/((153)) = 1/((17))`
`⇒x = 85/17 = 5, y = 153/17 = 9`
Hence, x = 5 and y = 9 is the required solution.
APPEARS IN
RELATED QUESTIONS
Which of the following pairs of linear equations has unique solution, no solution, or infinitely many solutions. In case there is a unique solution, find it by using cross multiplication method
x – 3y – 3 = 0
3x – 9y – 2 = 0
Form the pair of linear equations in the following problems and find their solutions (if they exist) by any algebraic method :
A part of monthly hostel charges is fixed and the remaining depends on the number of days one has taken food in the mess. When a student A takes food for 20 days she has to pay Rs 1000 as hostel charges whereas a student B, who takes food for 26 days, pays Rs 1180 as hostel charges. Find the fixed charges and the cost of food per day.
Solve the following systems of equations:
`4/x + 3y = 14`
`3/x - 4y = 23`
Solve each of the following systems of equations by the method of cross-multiplication
`(x + y)/(xy) = 2`
`(x - y)/(xy) = 6`
Solve each of the following systems of equations by the method of cross-multiplication
`(a - b)x + (a + b)y = 2a^2 - 2b^2`
(a + b)(a + y) = 4ab
Solve each of the following systems of equations by the method of cross-multiplication :
`57/(x + y) + 6/(x - y) = 5`
`38/(x + y) + 21/(x - y) = 9`
Solve each of the following systems of equations by the method of cross-multiplication :
6(ax + by) = 3a + 2b
6(bx - ay) = 3b - 2a
Solve the system of equations by using the method of cross multiplication:
3x + 2y + 25 = 0, 2x + y + 10 = 0
A person, rowing at the rate of 5 km/h in still water, takes thrice as much time in going 40 km upstream as in going 40 km downstream. Find the speed of the stream.
For what values of k will the following pair of linear equations have infinitely many solutions?
kx + 3y – (k – 3) = 0
12x + ky – k = 0
