Advertisements
Advertisements
Question
Form the pair of linear equations in the following problems and find their solutions (if they exist) by any algebraic method :
A part of monthly hostel charges is fixed and the remaining depends on the number of days one has taken food in the mess. When a student A takes food for 20 days she has to pay Rs 1000 as hostel charges whereas a student B, who takes food for 26 days, pays Rs 1180 as hostel charges. Find the fixed charges and the cost of food per day.
Solution
Let x be the fixed charge of the food and y be the charge for food per day.
According to the question,
x + 20y = 1000 ... (i)
x + 26y = 1180 ... (ii)
Subtracting equation (i) from equation (ii), we get
6y = 180
y = 180/6 = 30
Putting this value in equation (i), we get
x + 20 × 30 = 1000
x = 1000 - 600
x = 400
Hence, fixed charge = Rs 400 and charge per day = Rs 30
APPEARS IN
RELATED QUESTIONS
A train travels at a certain average speed for a distance of 54 km and then travels a distance of 63 km at an average speed of 6 km/h more than the first speed. If it takes 3 hours to complete the total journey, what is its first speed?
A thief, after committing a theft, runs at a uniform speed of 50 m/minute. After 2 minutes, a policeman runs to catch him. He goes 60 m in first minute and increases his speed by 5 m/minute every succeeding minute. After how many minutes, the policeman will catch the thief?
Solve the following system of equations by the method of cross-multiplication.
11x + 15y = – 23; 7x – 2y = 20
Solve the following systems of equations:
`1/(7x) + 1/(6y) = 3`
`1/(2x) - 1/(3y) = 5`
Solve the following systems of equations:
`1/(2x) + 1/(3y) = 2`
`1/(3x) + 1/(2y) = 13/6`
Solve each of the following systems of equations by the method of cross-multiplication
`(x + y)/(xy) = 2`
`(x - y)/(xy) = 6`
Solve each of the following systems of equations by the method of cross-multiplication :
`2/x + 3/y = 13`
`5/4 - 4/y = -2`
where `x != 0 and y != 0`
Find the values of x and y in the following rectangle [see figure].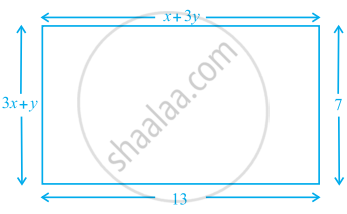
Solve the following pair of equations:
43x + 67y = – 24, 67x + 43y = 24
A person, rowing at the rate of 5 km/h in still water, takes thrice as much time in going 40 km upstream as in going 40 km downstream. Find the speed of the stream.
