Advertisements
Advertisements
प्रश्न
Solve each of the following systems of equations by the method of cross-multiplication :
`x(a - b + (ab)/(a - b)) = y(a + b - (ab)/(a + b))`
`x + y = 2a^2`
उत्तर
The solution of the systems of equation by the method of cross-multiplication:
Here we have the pair of simultaneous equation
`x(a - b + (ab)/(a - b)) = y(a + b - (ab)/(a + b)) = 0`
`x + y = 2a^2 = 0`
By cross multiplication method we get
`x/((-2a^2)xx-((a + b)- (ab)/(a + b)) - 0) = (-y)/((-2a^2)xx((a - b) + (ab)/(a - b)) = 0)`
`= 1/((a - b)+ (ab)/(a - b) - (-((a + b) - (ab)/(a + b))))`
`x/((-2a^2)xx-((a+ b)^2 + ab)/(a + b)) = (-y)/((-2a^2)xx(((a - b)^2 + ab)/((a - b)))`
`= 1/((((a - b)^2 + ab)/(a - b)) - (-(((a + b)^2 - ab)/(a + b))`
`x/((-2a^2)xx-((a^2 + b^2 + 2ab) - ab)/(a + b)) = (-y)/((-2a^2)xx((a^2 + b^2 - 2ab) + ab)/(a - b))`
`= 1/((((a^2 + b^2 - 2ab) + ab)/(a - b)) - (-(((a^2 + b^2 + 2ab) - ab)/(a + b))`
`x/(((2a^4 + 2a^2b^2 + 2a^3b))/(a + b))= y/((2a^4 + 2a^2b^2 - 2a^3b)/(a - b))`
`= 1/(((a^2 + b^2 -ab )(a + b) + (a^2 + b^2 + ab)(a - b))/((a - b)(a + b)))`
`x/((2a^4 + 2a^2b^2 + 2a^3b)/(a + b)) = y/((2a^4 + 2a^2b^2 - 2a^3b)/(a - b)) = 1/(((2a^3)/((a - b)(a + b)))`
Consider the following
`x/((2a^4 + 2a^2b^2 + 2a^3b)/(a + b)) = 1/(((2a^3)/((a - b)(a + b))))`
`x = ((a^2 + b^2 + ab)(a - b))/a`
`x = ((a^2 + b^2 + ab)(a - b))/a`
`x = (a^3 + ab^2 + a^2b - b^3 -ab^2 - a^2b)/a`
`x = (a^3 - b^3)/a`
And
`y/((2^4 + 2a^2b^2 -2a^3b)/(a - b)) =1 /((2a^3)/((a -b)(a + b)))`
`y/((a^2 + b^2 - ab)/(a - b)) = 1/(a/((a - b)(a + b)))`
`y(a/((a - b)(a + b))) = (a^2 + b^2 - ab)/(a - b)`
`y = ((a^2 + b^2 - ab)(a + b))/a`
`y = (a^3 + b^3)/a`
Hence we get the value of `x = (a^3 - b^3)/a and y = (a^3 + b^3)/a`
APPEARS IN
संबंधित प्रश्न
A thief, after committing a theft, runs at a uniform speed of 50 m/minute. After 2 minutes, a policeman runs to catch him. He goes 60 m in first minute and increases his speed by 5 m/minute every succeeding minute. After how many minutes, the policeman will catch the thief?
Solve the following system of equations by cross-multiplication method ax + by = 1; `bx + ay = \frac{(a+b)^{2}}{a^{2}+b^{2}-1`
Solve the following system of equations by cross-multiplications method.
`a(x + y) + b (x – y) = a^2 – ab + b^2`
`a(x + y) – b (x – y) = a^2 + ab + b^2`
Form the pair of linear equations in the following problems and find their solutions (if they exist) by any algebraic method
Yash scored 40 marks in a test, getting 3 marks for each right answer and losing 1 mark for each wrong answer. Had 4 marks been awarded for each correct answer and 2 marks been deducted for each incorrect answer, then Yash would have scored 50 marks. How many questions were there in the test?
Solve the following systems of equations:
`x + 2y = 3/2`
`2x + y = 3/2`
Solve each of the following systems of equations by the method of cross-multiplication
x + ay = b
ax − by = c
Solve each of the following systems of equations by the method of cross-multiplication
5ax + 6by = 28
3ax + 4by = 18
Solve the system of equations by using the method of cross multiplication:
7x - 2y – 3 = 0,
`11x - 3/2 y – 8 = 0.`
Find the values of x and y in the following rectangle [see figure].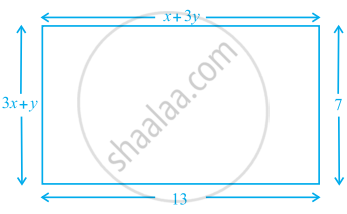
A two-digit number is obtained by either multiplying the sum of the digits by 8 and then subtracting 5 or by multiplying the difference of the digits by 16 and then adding 3. Find the number.
