Advertisements
Advertisements
Question
Solve the system of equations by using the method of cross multiplication:
`1/x + 1/y = 7, 2/x + 3/y = 17`
Solution
Taking `1/x = u and 1/y` = v, the given equations become:
u + v = 7
2u + 3v = 17
The given equations may be written as:
u + v – 7 = 0 …..(i)
2u + 3v – 17 = 0 ……(ii)
Here, `a_1 = 1, b_1 = 1, c_1 = -7, a_2 = 2, b_2 = 3 and c_2 = -17`
By cross multiplication, we have:
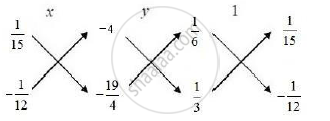
`∴ u/([1×(−17) −3 ×(−7)]) = v/([(−7) × 2 −1 ×(−17)] )= 1/([3−2])`
`⇒u/((−17+21) )= v/((−14+17)) = 1/(1)`
`⇒u/4 = v/3 = 1/1`
`⇒u = 4/1 = 4, v = 3/1 = 3`
`⇒ 1/x = 4, 1/y = 3`
`⇒ x = 1/4, y = 1/3`
Hence, x = `1/4 and y = 1/3` is the required solution.
APPEARS IN
RELATED QUESTIONS
Solve the following system of equations by cross-multiplication method.
ax + by = a – b; bx – ay = a + b
Solve the following system of equations by cross-multiplications method.
`a(x + y) + b (x – y) = a^2 – ab + b^2`
`a(x + y) – b (x – y) = a^2 + ab + b^2`
Form the pair of linear equations in the following problems and find their solutions (if they exist) by any algebraic method
The area of a rectangle gets reduced by 9 square units, if its length is reduced by 5 units and breadth is increased by 3 units. If we increase the length by 3 units and the breadth by 2 units, the area increases by 67 square units. Find the dimensions of the rectangle.
Solve the following systems of equations:
`sqrt2x + sqrt3y = 0`
`sqrt3x - sqrt8y = 0`
Solve each of the following systems of equations by the method of cross-multiplication
`x/a + y/b = 2`
`ax - by = a^2 - b^2`
Solve each of the following systems of equations by the method of cross-multiplication :
`ax + by = (a + b)/2`
3x + 5y = 4
Solve each of the following systems of equations by the method of cross-multiplication :
(a + 2b)x + (2a − b)y = 2
(a − 2b)x + (2a + b)y = 3
Solve each of the following systems of equations by the method of cross-multiplication :
6(ax + by) = 3a + 2b
6(bx - ay) = 3b - 2a
Solve the system of equations by using the method of cross multiplication:
3x - 2y + 3 = 0,
4x + 3y – 47 = 0
Solve the following pair of equations:
`x/a + y/b = a + b, x/a^2 + y/b^2 = 2, a, b ≠ 0`
