Advertisements
Advertisements
प्रश्न
Solve the following pair of equations:
`x/a + y/b = a + b, x/a^2 + y/b^2 = 2, a, b ≠ 0`
उत्तर
Given pair of linear equations is
`x/a + y/b` = a + b .....(i)
And `x/a^2 + y/b^2` = 2, a, b ≠ 0 ......(ii)
On multiplying equation (i) by `1/a` and then subtracting from equation (ii), we get
`x/a^2 + y/b^2 = 2`
`x/a^2 + y/(ab) = 1 + b/a`
– – –
`y(1/b^2 - 1/(ab)) = 2 - 1 - b/a`
⇒ `y((a - b)/(ab^2)) = 1 - b/a = ((a - b)/a)`
⇒ y = `(ab^2)/a`
⇒ y = b2
Now, put the value of y in equation (ii), we get
`x/a^2 + b^2/b^2` = 2
⇒ `x/a^2` = 2 – 1 = 1
⇒ x = a2
Hence, the required values of x and y are a2 and b2, respectively.
APPEARS IN
संबंधित प्रश्न
Solve each of the following systems of equations by the method of cross-multiplication
`x/a + y/b = 2`
`ax - by = a^2 - b^2`
Solve each of the following systems of equations by the method of cross-multiplication :
(a + 2b)x + (2a − b)y = 2
(a − 2b)x + (2a + b)y = 3
Solve each of the following systems of equations by the method of cross-multiplication
bx + cy = a + b
`ax (1/(a - b) - 1/(a + b)) + cy(1/(b -a) - 1/(b + a)) = (2a)/(a + b)`
Solve each of the following systems of equations by the method of cross-multiplication :
`b/a x + a/b y - (a^2 + b^2) = 0`
x + y - 2ab = 0
Solve the system of equations by using the method of cross multiplication:
2x + y – 35 = 0,
3x + 4y – 65 = 0
Solve the system of equation by using the method of cross multiplication:
`5/("x+y") - 2/("x− y") + 1 = 0, 15/("x+y") + 7/("x− y") – 10 = 0`
Find the values of x and y in the following rectangle [see figure].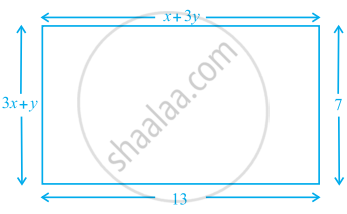
Solve the following pair of equations:
43x + 67y = – 24, 67x + 43y = 24
Solve the following pair of equations:
`(2xy)/(x + y) = 3/2, (xy)/(2x - y) = (-3)/10, x + y ≠ 0, 2x - y ≠ 0`
Anuj had some chocolates, and he divided them into two lots A and B. He sold the first lot at the rate of ₹ 2 for 3 chocolates and the second lot at the rate of ₹ 1 per chocolate, and got a total of ₹ 400. If he had sold the first lot at the rate of ₹ 1 per chocolate, and the second lot at the rate of ₹4 for 5 chocolates, his total collection would have been ₹460. Find the total number of chocolates he had.
