Advertisements
Advertisements
प्रश्न
Anuj had some chocolates, and he divided them into two lots A and B. He sold the first lot at the rate of ₹ 2 for 3 chocolates and the second lot at the rate of ₹ 1 per chocolate, and got a total of ₹ 400. If he had sold the first lot at the rate of ₹ 1 per chocolate, and the second lot at the rate of ₹4 for 5 chocolates, his total collection would have been ₹460. Find the total number of chocolates he had.
उत्तर
Let the number of chocolates in lot A be x
And let the number of chocolates in lot B be y
∴ Total number of chocolates = x + y
Price of 1 chocolate = ₹ `2/3`, so for x chocolates = `2/3`x and price of y chocolates at the rate of ₹ 1 per chocolate = y.
∴ By the given condition `2/3`x + y = 400
⇒ 2x + 3y = 1200 ......(i)
Similarly x + `4/5`y = 460
⇒ 5x + 4y = 2300 ......(ii)
By solving (i) and (ii) we get
x = 300 and y = 200
∴ x + y = 300 + 200 = 500
So, Anuj had 500 chocolates.
APPEARS IN
संबंधित प्रश्न
Solve the following system of equations by cross-multiplication method x + y = a – b; ax – by = a2 + b2
Form the pair of linear equations in the following problems and find their solutions (if they exist) by any algebraic method:
A fraction becomes `1/3` when 1 is subtracted from the numerator and it becomes `1/4` when 8 is added to its denominator. Find the fraction.
Solve the following systems of equations:
4u + 3y = 8
`6u - 4y = -5`
Solve the following systems of equations:
`x + y/2 = 4`
`x/3 + 2y = 5`
Solve the following systems of equations:
`sqrt2x + sqrt3y = 0`
`sqrt3x - sqrt8y = 0`
Solve the following systems of equations:
`1/(7x) + 1/(6y) = 3`
`1/(2x) - 1/(3y) = 5`
Solve each of the following systems of equations by the method of cross-multiplication
`(x + y)/(xy) = 2`
`(x - y)/(xy) = 6`
A father's age is three times the sum of the ages of his two children. After 5 years his age will be two times the sum of their ages. Find the present age of the father.
Find the values of x and y in the following rectangle [see figure].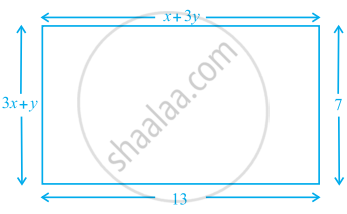
A shopkeeper sells a saree at 8% profit and a sweater at 10% discount, thereby, getting a sum Rs 1008. If she had sold the saree at 10% profit and the sweater at 8% discount, she would have got Rs 1028. Find the cost price of the saree and the list price (price before discount) of the sweater.
