Advertisements
Advertisements
प्रश्न
A motorboat whose speed in still water is 18 km/h, takes 1 hour more to go 24 km upstream than to return downstream to the same spot. Find the speed of the stream.
उत्तर
Solution:
Let speed of stream = x km/h
Speed of boat in still water = 18 km/h
Speed of boat in upstream = (18 –x )km/h
Speed of boat in downstream = (18 + x ) km/h
Distance = 24 km
As per question, it takes 1 hour more to go upstream 24 km, than downstream
24 km /(18 –x ) = 24 km/(18 + x ) + 1
x2 + 48x – 324 = 0
x = 6 or x = – 54
But, as speed can not be negative
Hence, the speed of stream = 6 km/h
संबंधित प्रश्न
A thief runs with a uniform speed of 100 m/minute. After one minute, a policeman runs after the thief to catch him. He goes with a speed of 100 m/minute in the first minute and increases his speed by 10 m/minute every succeeding minute. After how many minutes the policeman will catch the thief.
Solve the follownig system of equations by the method of cross-multiplication.
2x – 6y + 10 = 0
3x – 7y + 13 = 0
Solve the following system of equations by the method of cross-multiplication.
11x + 15y = – 23; 7x – 2y = 20
Solve the following system of equations by cross-multiplication method x + y = a – b; ax – by = a2 + b2
Form the pair of linear equations in the following problems and find their solutions (if they exist) by any algebraic method :
A part of monthly hostel charges is fixed and the remaining depends on the number of days one has taken food in the mess. When a student A takes food for 20 days she has to pay Rs 1000 as hostel charges whereas a student B, who takes food for 26 days, pays Rs 1180 as hostel charges. Find the fixed charges and the cost of food per day.
Form the pair of linear equations in the following problems and find their solutions (if they exist) by any algebraic method:
A fraction becomes `1/3` when 1 is subtracted from the numerator and it becomes `1/4` when 8 is added to its denominator. Find the fraction.
Form the pair of linear equations in the following problems and find their solutions (if they exist) by any algebraic met
Places A and B are 100 km apart on a highway. One car starts from A and another from B at the same time. If the cars travel in the same direction at different speeds, they meet in 5 hours. If they travel towards each other, they meet in 1 hour. What are the speeds of the two cars?
Solve the following systems of equations:
`x/3 + y/4 =11`
`(5x)/6 - y/3 = -7`
Solve the following systems of equations:
`1/(7x) + 1/(6y) = 3`
`1/(2x) - 1/(3y) = 5`
Solve the following systems of equations:
`4/x + 3y = 14`
`3/x - 4y = 23`
Solve each of the following systems of equations by the method of cross-multiplication :
x + 2y + 1 = 0
2x − 3y − 12 = 0
Solve each of the following systems of equations by the method of cross-multiplication
`x/a + y/b = 2`
`ax - by = a^2 - b^2`
Solve each of the following systems of equations by the method of cross-multiplication
bx + cy = a + b
`ax (1/(a - b) - 1/(a + b)) + cy(1/(b -a) - 1/(b + a)) = (2a)/(a + b)`
Solve each of the following systems of equations by the method of cross-multiplication
`(a - b)x + (a + b)y = 2a^2 - 2b^2`
(a + b)(a + y) = 4ab
Solve each of the following systems of equations by the method of cross-multiplication :
6(ax + by) = 3a + 2b
6(bx - ay) = 3b - 2a
Solve the system of equations by using the method of cross multiplication:
x + 2y + 1 = 0,
2x – 3y – 12 = 0.
Solve the system of equations by using the method of cross multiplication:
6x - 5y - 16 = 0,
7x - 13y + 10 = 0
Solve the system of equations by using the method of cross multiplication:
2x + y – 35 = 0,
3x + 4y – 65 = 0
Solve the system of equations by using the method of cross multiplication:
`x/6 + y/15 – 4 = 0, x/3 - y/12 – 19/4 = 0`
Solve the system of equations by using the method of cross multiplication:
`1/x + 1/y = 7, 2/x + 3/y = 17`
Solve the system of equations by using the method of cross multiplication:
`a/x - b/y = 0, (ab^2)/x + (a^2b)/y = (a^2 + b^2), where x ≠ 0 and y ≠ 0.`
Find the values of x and y in the following rectangle [see figure].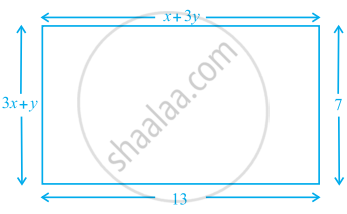
Solve the following pair of equations:
`4x + 6/y = 15, 6x - 8/y = 14, y ≠ 0`
Solve the following pair of equations:
`x/a + y/b = a + b, x/a^2 + y/b^2 = 2, a, b ≠ 0`
In a competitive examination, one mark is awarded for each correct answer while `1/2` mark is deducted for every wrong answer. Jayanti answered 120 questions and got 90 marks. How many questions did she answer correctly?
Ankita travels 14 km to her home partly by rickshaw and partly by bus. She takes half an hour if she travels 2 km by rickshaw, and the remaining distance by bus. On the other hand, if she travels 4 km by rickshaw and the remaining distance by bus, she takes 9 minutes longer. Find the speed of the rickshaw and of the bus.
A two-digit number is obtained by either multiplying the sum of the digits by 8 and then subtracting 5 or by multiplying the difference of the digits by 16 and then adding 3. Find the number.
Susan invested certain amount of money in two schemes A and B, which offer interest at the rate of 8% per annum and 9% per annum, respectively. She received Rs 1860 as annual interest. However, had she interchanged the amount of investments in the two schemes, she would have received Rs 20 more as annual interest. How much money did she invest in each scheme?
