Advertisements
Advertisements
प्रश्न
Solve the system of equations by using the method of cross multiplication:
2x + y – 35 = 0,
3x + 4y – 65 = 0
उत्तर
The given equations may be written as:
2x + y – 35 = 0 …….(i)
3x + 4y – 65 = 0 …….(ii)
Here a1 = 2, b1 = 1, c1 = -35, a2 = 3, b2 = 4 and c2 = -65
By cross multiplication, we have:
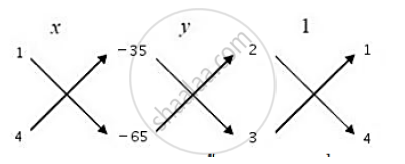
`∴ x/((1×(−65) −4 ×(−35)]) = Y/([(−35) × 3 −(−65) × 2]) = 1/([2 × 4−3 × 1])`
`⇒x/((−65+140) )= y/((−105+130) )= 1/((8−3))`
`⇒x/75 = y/25 = 1/5`
`⇒ x = 75/5 = 15, y = 25/5 = 5`
Hence, x = 15 and y = 5 is the required solution.
APPEARS IN
संबंधित प्रश्न
Solve the following system of equations by cross-multiplication method ax + by = 1; `bx + ay = \frac{(a+b)^{2}}{a^{2}+b^{2}-1`
For which values of a and b does the following pair of linear equations have an infinite number of solutions?
2x + 3y = 7
(a – b) x + (a + b) y = 3a + b – 2
For which value of k will the following pair of linear equations have no solution?
3x + y = 1
(2k – 1)x + (k – 1)y = 2k + 1
Solve the following pair of linear equations by the substitution and cross-multiplication methods
8x + 5y = 9
3x + 2y = 4
Solve the following systems of equations:
4u + 3y = 8
`6u - 4y = -5`
Solve the following systems of equations:
`1/(7x) + 1/(6y) = 3`
`1/(2x) - 1/(3y) = 5`
Solve each of the following systems of equations by the method of cross-multiplication :
`ax + by = (a + b)/2`
3x + 5y = 4
Solve the system of equations by using the method of cross multiplication:
2ax + 3by – (a + 2b) = 0,
3ax + 2by – (2a + b) = 0
Solve the following pair of equations:
`x/3 + y/4 = 4, (5x)/6 - y/4 = 4`
Solve the following pair of equations:
43x + 67y = – 24, 67x + 43y = 24
