Advertisements
Advertisements
Question
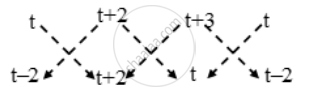
Prove that the area of a triangle with vertices (t, t −2), (t + 2, t + 2) and (t + 3, t) is independent of t.
Solution 1
Let A(t, t − 2), B(t + 2, t + 2) and C(t + 2, t) be the vertices of the given triangle.
We know that the area of the triangle having vertices (x1, y1), (x2, y2) and (x3, y3) is
`1/2|x_1(y_2-y_3)+x^2(y_3-y_1)+x_3(y_1-y_2)||`
∴ Area of ∆ABC = `|1/2[x_1(y_2-y_3)+x^2(y_3-y_1)+x_3(y_1-y_2)||`
`=|1/2[t(t+2−t)+(t+2)(t−t+2)+(t+3)(t−2−t−2)]|`
`|1/2(2t+2t+4−4t−12)|`
`|-4|`
=4 square units
Hence, the area of the triangle with given vertices is independent of t.
Solution 2
`therefore `
`rArr `
`rArr`
`rArr`
⇒ Area of ∆ABC = 4 sq. units
Hence, Area of ∆ABC is independent of t.
APPEARS IN
RELATED QUESTIONS
Find the area of the triangle PQR with Q(3,2) and the mid-points of the sides through Q being (2,−1) and (1,2).
Find the area of the following triangle:

Find the area of a triangle whose vertices are
(a, c + a), (a, c) and (−a, c − a)
The vertices of ΔABC are (−2, 1), (5, 4) and (2, −3) respectively. Find the area of the triangle and the length of the altitude through A.
Prove that (2, -2) (-2, 1) and (5, 2) are the vertices of a right-angled triangle. Find the area of the triangle and the length of the hypotenuse.
The area of a triangle is 5. Two of its vertices are (2, 1) and (3, −2). The third vertex lies on y = x + 3. Find the third vertex.
Show that the following points are collinear:
(i) A(2,-2), B(-3, 8) and C(-1, 4)
Find the value of x for which points A(x, 2), B(-3, -4) and C(7, -5) are collinear.
If the area of triangle ABC formed by A(x, y), B(1, 2) and C(2, 1) is 6 square units, then prove that x + y = 15 ?
The table given below contains some measures of the right angled triangle. Find the unknown values.
| Base | Height | Area |
| 20 cm | 40 cm | ? |
