Advertisements
Advertisements
प्रश्न
If the points A (x, y), B (3, 6) and C (−3, 4) are collinear, show that x − 3y + 15 = 0.
उत्तर
If the given points A (x, y), B (3, 6) and C (−3, 4) are collinear, then
Area of the triangle ΔABC = 0
`therefore 1/2 [x_1(y_2-y_3)+x_2(y_3-y_3)+x_3(y_1-y_2)]=0`
`rArrx(6-4)+3(4-y)+(-3)(y-6)=0`
`rArr2x+12-3y-3y+18=0`
`rArr2x-6y+30=0`
`rArr2(x-3y+15)=0`
`rArrx-3y+15=0`
APPEARS IN
संबंधित प्रश्न
Find the area of the following triangle:
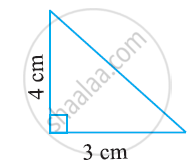
Find the area of the following triangle:
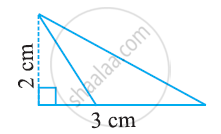
Find the missing value:
| Base | Height | Area of triangle |
| 15 cm | ______ | 87 cm2 |
Find the area of a triangle whose vertices are
(a, c + a), (a, c) and (−a, c − a)
Show that the following sets of points are collinear.
(1, −1), (2, 1) and (4, 5)
Two vertices of a triangle are (1, 2), (3, 5) and its centroid is at the origin. Find the coordinates of the third vertex.
Prove analytically that the line segment joining the middle points of two sides of a triangle is equal to half of the third side.
If the centroid of ΔABC having vertices A (a,b) , B (b,c) and C (c,a) is the origin, then find the value of (a+b+c).
The area of the triangle whose vertices are A(1, 2), B(-2, 3) and C(-3, -4) is ______.
Observe all the four triangles FAB, EAB, DAB and CAB as shown in the given figure.

- All triangles have the same base and the same altitude.
- All triangles are congruent.
- All triangles are equal in area.
- All triangles may not have the same perimeter.
