Advertisements
Advertisements
प्रश्न
Find the relation between x and y if, the points A(x, y), B(-5, 7) and C(-4, 5) are collinear.
उत्तर
Given, the pointsA(x,y), B(-5,7) and C(-4,5) are collinear.
So, the area formed by these vertices is 0.
1/2[x(7-5)+(-5)(5-y)+(-4)(y-7)= 0
1/2[2x-25+5y-4y+28]= 0
1/2[2x+y+3]= 0
2x+y+3 = 0
y = -2x- 3
APPEARS IN
संबंधित प्रश्न
Prove that the area of a triangle with vertices (t, t −2), (t + 2, t + 2) and (t + 3, t) is independent of t.
The vertices of ∆ABC = are A (4, 6), B(1, 5) and C(7, 2). A line is drawn to intersect sides AB and AC at D and E respectively such that `\frac{AD}{AB}=\frac{AE}{AC}=\frac{1}{4}` .Calculate the area of ∆ADE and compare it with the area of ∆ABC
Find the area of the triangle whose vertices are: (–5, –1), (3, –5), (5, 2)
The perimeter of a triangular field is 540 m and its sides are in the ratio 25 : 17 : 12. Find the area of the triangle ?
Show that the following points are collinear:
A(-5,1), B(5, 5) and C(10, 7)
If Δ = `|(1, x, x^2),(1, y, y^2),(1, z, z^2)|`, Δ1 = `|(1, 1, 1),(yz, zx, xy),(x, y, z)|`, then prove that ∆ + ∆1 = 0.
The value of the determinant `abs((1,"x","x"^3),(1,"y","y"^3),(1,"z","z"^3))` is ____________.
If the points (a1, b1), (a2, b2) and(a1 + a2, b1 + b2) are collinear, then ____________.
Find the area of the trapezium PQRS with height PQ given in the following figure.
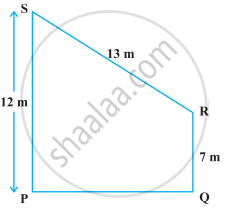
Area of a triangle = `1/2` base × ______.
