Advertisements
Advertisements
प्रश्न
Find the angle subtended at the origin by the line segment whose end points are (0, 100) and (10, 0).
उत्तर
Let the given points be A(0,100), B(10,0) and the origin be denoted by o(0,0)
We know that
In a right angled triangle the angle oppposite the hypotenuse subtend an angle of 90°
Let us find distance AB, AO, BO
`AB = sqrt((10 - 0)^2 + (0 - 100)^2)`
`= sqrt(100 + 10000)`
`= sqrt(10100)` units
`AO = sqrt((0 - 0)^2 + (0 - 100)^2)`
= `sqrt(100)` untis
Her we can see that, `AO^2 + BO^2 = AB^2`
Therefore, ΔAOB is a right angled triangle with AB being the hypotenuse.
So the angle subtended at the origin by the giving line segment is 90°
APPEARS IN
संबंधित प्रश्न
If P(–5, –3), Q(–4, –6), R(2, –3) and S(1, 2) are the vertices of a quadrilateral PQRS, find its area.
If the points P(–3, 9), Q(a, b) and R(4, – 5) are collinear and a + b = 1, find the values of a and b.
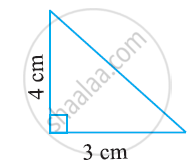
Find the area of the following triangle:
If A(–5, 7), B(–4, –5), C(–1, –6) and D(4, 5) are the vertices of a quadrilateral, find the area of the quadrilateral ABCD
Find the area of a triangle whose vertices are
`(at_1^2,2at_1),(at_2^2,2at_2)` and `(at_3^2,2at_3)`
Four points A (6, 3), B (−3, 5), C(4, −2) and D (x, 3x) are given in such a way that `(ΔDBG) /(ΔABG)=1/2,` find x
Prove that the lines joining the middle points of the opposite sides of a quadrilateral and the join of the middle points of its diagonals meet in a point and bisect one another
If the coordinates of the mid-points of the sides of a triangle are (1, 1), (2, —3) and (3, 4), find the vertices of the triangle.
The table given below contains some measures of the right angled triangle. Find the unknown values.
| Base | Height | Area |
| ? | 12 m | 24 sq.m |
The area of ∆ABC is 8 cm2 in which AB = AC = 4 cm and ∠A = 90º.
