Advertisements
Advertisements
प्रश्न
Show that the ∆ABC is an isosceles triangle if the determinant
Δ = `[(1, 1, 1),(1 + cos"A", 1 + cos"B", 1 + cos"C"),(cos^2"A" + cos"A", cos^2"B" + cos"B", cos^2"C" + cos"C")]` = 0
उत्तर
We have, Δ = `[(1, 1, 1),(1 + cos"A", 1 + cos"B", 1 + cos"C"),(cos^2"A" + cos"A", cos^2"B" + cos"B", cos^2"C" + cos"C")]` = 0
[Applying C1 → C1 – C2 and C2 → C2 – C3]
⇒ `[(0, 0, 1),(cos"A" - cos"C", cos"B" - cos"C", 1 + cos"C"),(cos^2"A" + cos"A" - cos^2"C" - cos"C", cos^2"B" + cos"B" - cos^2"C" - cos"C", cos^2"C" + cos"C")]` = 0
[Taking (cos A – cos C) common from C1 and (cos B – cos C) common from C2]
⇒ `(cos "A" - cos "C") (cos "B" - cos "C") xx [(0, 0, 1),(1, 1, 1 + cos"C"),(cos"A" + cos"C" + 1, cos"B" + cos"C" + 1, cos^2"C" + cos"C")]` = 0
[Applying C1 → C1 – C2]
⇒ `(cos "A" - cos "C") (cos "B" - cos "C") xx [(0, 0, 1),(0, 1, 1 + cos"C"),(cos"A" - cos"B", cos"B" + cos"C" + 1, cos^2"C" + cos"C")]` = 0
⇒ `(cos"A" - cos"C")(cos"B" - cos"C")(cos"B" - cos"A")` = 0
⇒ cos A = cos C or cos B = cos C or cos B = cos A
⇒ A = C or B = C or B = A
Hence, ΔABC is an isosceles triangle.
APPEARS IN
संबंधित प्रश्न
Prove that the area of a triangle with vertices (t, t −2), (t + 2, t + 2) and (t + 3, t) is independent of t.
If P(–5, –3), Q(–4, –6), R(2, –3) and S(1, 2) are the vertices of a quadrilateral PQRS, find its area.
If the points P(–3, 9), Q(a, b) and R(4, – 5) are collinear and a + b = 1, find the values of a and b.
The vertices of ∆ABC = are A (4, 6), B(1, 5) and C(7, 2). A line is drawn to intersect sides AB and AC at D and E respectively such that `\frac{AD}{AB}=\frac{AE}{AC}=\frac{1}{4}` .Calculate the area of ∆ADE and compare it with the area of ∆ABC
For what value of x will the points (x, –1), (2, 1) and (4, 5) lie on a line ?
Find the area of the triangle whose vertices are: (2, 3), (-1, 0), (2, -4)
In each of the following find the value of 'k', for which the points are collinear.
(8, 1), (k, -4), (2, -5)
The class X students of a secondary school in Krishinagar have been allotted a rectangular plot of land for their gardening activity. Saplings of Gulmohar are planted on the boundary at a distance of 1 m from each other. There is a triangular grassy lawn in the plot as shown in the following figure. The students are to sow seeds of flowering plants on the remaining area of the plot.

(i) Taking A as origin, find the coordinates of the vertices of the triangle.
(ii) What will be the coordinates of the vertices of Δ PQR if C is the origin?
Also calculate the areas of the triangles in these cases. What do you observe?
The vertices of a ΔABC are A (4, 6), B (1, 5) and C (7, 2). A line is drawn to intersect sides AB and AC at D and E respectively, such that `(AD)/(AB) = (AE)/(AC) = 1/4`Calculate the area of the ΔADE and compare it with the area of ΔABC. (Recall Converse of basic proportionality theorem and Theorem 6.6 related to ratio of areas of two similar triangles)
Find values of k if area of triangle is 4 square units and vertices are (−2, 0), (0, 4), (0, k)
The perimeter of a triangular field is 540 m and its sides are in the ratio 25 : 17 : 12. Find the area of the triangle ?
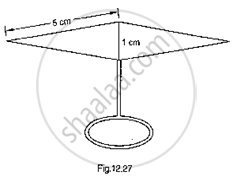
Find the area of the blades of thc magnetic compass shown in Fig.. 12.27. (Take √11 = 3.32).
Show that the points A(-5,6), B(3,0) and C(9,8) are the vertices of an isosceles right-angled triangle. Calculate its area.
If G(-2, 1) is the centroid of a ΔABC and two of its vertices are A(1, -6) and B(-5, 2) , find the third vertex of the triangle.
Find the area of Δ ABC whose vertices are:
A (1,2) B (-2,3) and C (-3,-4)
Find the area of ΔABC with A(1, -4) and midpoints of sides through A being (2, -1) and (0, -1).
A(6,1) , B(8,2) and C(9,4) are the vertices of a parallelogram ABCD. If E is the midpoint of DC, find the area of ΔADE
Find the value of k so that the area of the triangle with vertices A (k+1, 1), B(4, -3) and C(7, -k) is 6 square units
Find the value of y for which the points A(-3, 9), B(2,y) and C(4,-5) are collinear.

In Figure 1, PS = 3 cm, QS = 4 cm, ∠PRQ = θ, ∠PSQ = 90°, PQ ⊥ RQ and RQ = 9 cm. Evaluate tan θ.
What is the area of a triangle with base 4.8 cm and height 3.6 cm?
The table given below contains some measures of the right angled triangle. Find the unknown values.
| Base | Height | Area |
| ? | 12 m | 24 sq.m |
Let ∆ = `|("A"x, x^2, 1),("B"y, y^2, 1),("C"z, z^2, 1)|`and ∆1 = `|("A", "B", "C"),(x, y, z),(zy, zx, xy)|`, then ______.
If the co-ordinates of the vertices of an equilateral triangle with sides of length ‘a’ are (x1, y1), (x2, y2), (x3, y3), then `|(x_1, y_1, 1),(x_2, y_2, 1),(x_3, y_3, 1)|^2 = (3"a"^4)/4`
The area of a triangle with vertices (a, b + c), (b, c + a) and (c, a + b) is ______.
The area of the triangle whose vertices are A(1, 2), B(-2, 3) and C(-3, -4) is ______.
Find the coordinates of the point Q on the x-axis which lies on the perpendicular bisector of the line segment joining the points A(–5, –2) and B(4, –2). Name the type of triangle formed by the points Q, A and B.
The points A(2, 9), B(a, 5) and C(5, 5) are the vertices of a triangle ABC right angled at B. Find the values of a and hence the area of ∆ABC.
The base and the corresponding altitude of a parallelogram are 10 cm and 3.5 cm, respectively. The area of the parallelogram is 30 cm2.
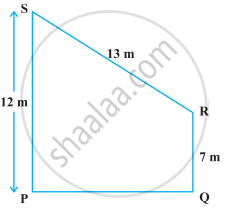
Find the area of the trapezium PQRS with height PQ given in the following figure.